Giải mục II trang 117, 118 SGK Toán 7 tập 2 - Cánh diều
II. Tính chất ba đường cao của tam giác
II. Tính chất ba đường cao của tam giác
HĐ 2
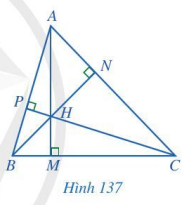
Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137) , cho biết ba đường cao đó có cùng đi qua một điểm hay không.
Phương pháp giải:
Quan sát Hình 137 để xem ba đường cao AM, BN, CP có cùng đi qua một điểm hay không.
Lời giải chi tiết:
Ba đường cao AM, BN, CP có cùng đi qua một điểm là điểm H .
LT - VD 2
Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC .
Phương pháp giải:
Chứng minh G là trực tâm của tam giác ABC bằng cách chứng minh G là giao điểm của ba đường cao của tam giác ABC .
Lời giải chi tiết:
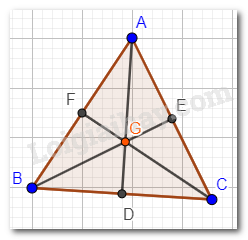
Tam giác ABC đều nên AB = AC = BC .
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD .
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD ( D là trung điểm của đoạn thẳng BC ).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF .
Vậy G cũng là trực tâm của tam giác ABC .
LT - VD 3
Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
Phương pháp giải:
Chứng minh AB = AC = BC
Lời giải chi tiết:
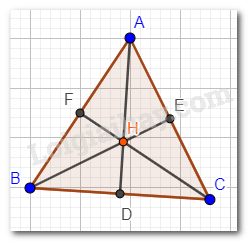
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC . Ta phải chứng minh tam giác ABC đều.
Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD;
\(AD \bot BC; BE \bot AC; CF \bot AB\)
Xét tam giác ADB và tam giác ADC có:
AD chung
\(\widehat{ADB}=\widehat{ADC} (=90^0)\)
BD = CD ( D là trung điểm của đoạn thẳng BC ).
Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).
Tương tự, ta cũng được, AC = BC
Xét tam giác ABC có AB = AC = BC nên là tam giác đều.
Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.