Giải mục II trang 105, 106 SGK Toán 7 tập 2 - Cánh diều
II. Tính chất ba đường trung tuyến của tam giác
II. Tính chất ba đường trung tuyến của tam giác
HĐ 2
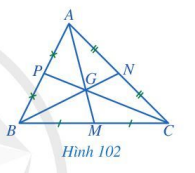
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102 , cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không.
Phương pháp giải:
Quan sát Hình 102 để xem ba đường trung tuyến có cùng đi qua một điểm hay không.
Lời giải chi tiết:
Ba đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G .
LT - VD 2
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G . Gọi I là trung điểm của cạnh QR . Chứng minh rằng ba điểm P, G, I thẳng hàng.
Phương pháp giải:
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G . Gọi I là trung điểm của cạnh QR . Chứng minh rằng ba điểm P, G, I thẳng hàng.
Lời giải chi tiết:
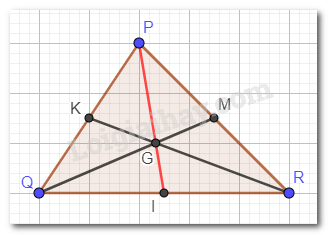
Ta có G là giao điểm của hai đường trung tuyến QM và RK .
Mà I là trung điểm của QR nên PI cũng là đường trung tuyến trong tam giác PQR .
Vậy PI giao với QM và RK tại G
Do đó, G thuộc PI hay ba điểm P, G, I thẳng hàng.
HĐ 3
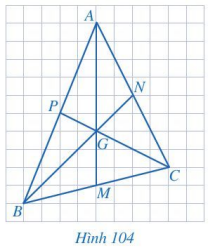
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104 . Bằng cách đếm số ô vuông, tìm các tỉ số
\(\dfrac{{AG}}{{AM}},\dfrac{{BG}}{{BN}},\dfrac{{CG}}{{CP}}\).
Phương pháp giải:
Quan sát Hình 104 rồi đếm số ô vuông của mỗi cạnh tương ứng để đưa ra các tỉ số.
Lời giải chi tiết:
Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).