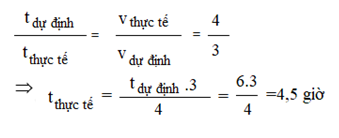Giải mục II trang 65, 66 SGK Toán 7 tập 1 - Cánh diều
Cho biết x, y là hai đại lượng tỉ lệ nghịch với nhau:
Hoạt động 2
Cho biết x, y là hai đại lượng tỉ lệ nghịch với nhau:
|
x |
x 1 = 20 |
x 2 = 18 |
x 3 = 15 |
x 4 = 5 |
|
y |
y 1 = 9 |
y 2 = ? |
y 3 = ? |
y 4 = ? |
a) Hãy xác định hệ số tỉ lệ
b) Tìm số thích hợp cho ? trong bảng trên
c) So sánh các tỉ số: x 1 y 1 ; x 2 y 2 ; x 3 y 3 ; x 4 y 4 .
d) So sánh các tỉ số: \(\frac{{{x_1}}}{{{x_2}}}\) và \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\) và \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) và \(\frac{{{y_4}}}{{{y_3}}}\)
Phương pháp giải:
+ Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = \frac{a}{x}\) hay x.y = a (a là hằng số khác 0) thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a
+ Tính các tích rồi so sánh
+ Tính các tỉ số rồi so sánh
Lời giải chi tiết:
a) Hệ số tỉ lệ a = x 1 .y 1 = 20. 9 =180
b) Ta có: y= \(\frac{{180}}{x}\)
Khi x 2 = 18 thì y 2 = \(\frac{{180}}{{{x_2}}} = \frac{{180}}{{18}} = 10\)
Khi x 3 = 15 thì y 3 = \(\frac{{180}}{{{x_3}}} = \frac{{180}}{{15}} = 12\)
Khi x 4 = 18 thì y 4 = \(\frac{{180}}{{{x_4}}} = \frac{{180}}{5} = 36\)
c) Tích x 1 .y 1 = 20. 9 =180
x 2 .y 2 = 18.10 =180
x 3 .y 3 = 15.12 =180
x 4 .y 4 = 5.36 =180
Vậy x 1 y 1 = x 2 y 2 = x 3 y 3 = x 4 y 4 =180
d) Ta có:
\(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{20}}{{18}}\)=\(\frac{{10}}{9}\) ; \(\frac{{{y_2}}}{{{y_1}}}\)= \(\frac{{10}}{9}\)
\(\frac{{{x_1}}}{{{x_3}}}\) = \(\frac{{20}}{{15}}\)=\(\frac{4}{3}\) ; \(\frac{{{y_3}}}{{{y_1}}}\) = \(\frac{{12}}{9}\) = \(\frac{4}{3}\)
\(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{15}}{5}\) = 3; \(\frac{{{y_4}}}{{{y_3}}}\)= \(\frac{{36}}{{12}}\) = 3
Vậy \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{x_3}}}\)= \(\frac{{{y_3}}}{{{y_1}}}\); \(\frac{{{x_3}}}{{{x_4}}}\) = \(\frac{{{y_4}}}{{{y_3}}}\)
Luyện tập vận dụng 2
Một ô tô dự định đi từ A đến B trong 6 giờ. Nhưng thực tế ô tô đi với vận tốc gấp \(\frac{4}{3}\) vận tốc dự định. Tính thời gian ô tô đã đi.
Phương pháp giải:
Thời gian ô tô đi và vận tốc đi trên cùng 1 quãng đường là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: \(\frac{{{x_1}}}{{{x_2}}}\) = \(\frac{{{y_2}}}{{{y_1}}}\)
Lời giải chi tiết:
Vì v. t = s không đổi nên vận tốc và thời gian ô tô đi là 2 đại lượng tỉ lệ nghịch
Theo tính chất 2 đại lượng tỉ lệ nghịch, ta có: