Giải phần B. Kết nối - Bài tập phát triển năng lực Toán 5 — Không quảng cáo

Câu 7

Viết số thích hợp vào chỗ chấm:

Phương pháp giải:

Áp dụng các cách đổi:

Lời giải chi tiết:

Câu 8

Điền dấu >, <, = thích hợp vào chỗ chấm:

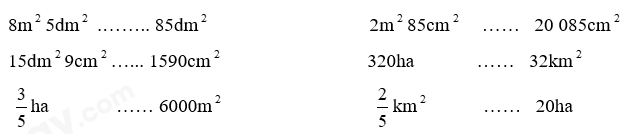
Phương pháp giải:

Áp dụng cách đổi:

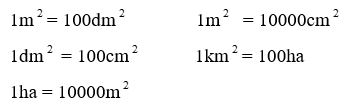
Lời giải chi tiết:

Câu 9

Để lát nền một căn phòng cần 240 viên gạch vân gỗ hình vuông có cạnh 50cm. Hỏi căn phòng đó có diện tích bao nhiêu mét vuông? (Biết phần mạch vữa không đáng kể)

Phương pháp giải:

Diện tích mỗi viên gạch = cạnh x cạnh

Diện tích căn phòng = diện tích mỗi viên gạch x số viên gạch

Lời giải chi tiết:

Diện tích mỗi viên gạch là:

50 x 50 = 2500 (cm ² )

Diện tích căn phòng đó là:

2500 x 240 = 600000 (cm ² )

Đổi 600 000cm ² = 60m ²

Đáp số: 60m ²

Câu 10

Một thửa ruộng hình chữ nhật có chu vi bằng 180m, chiều dài bằng $\frac{5}{4}$ chiều rộng.

a) Tính chiều dài và chiều rộng của thửa ruộng đó.

b) Biết rằng cứ 100m ² thu hoạch được 70kg thóc. Hỏi trên tất cả thửa ruộng đó người ta thu hoạch được bao nhiêu tạ thóc?

Phương pháp giải:

a)

- Tìm nửa chu vi thửa ruộng = chu vi hình chữ nhật : 2

- Vẽ sơ đồ, tìm tổng số phần bằng nhau

- Chiều dài = nửa chu vi : số phần bằng nhau x 5

- Chiều rộng = Nửa chu vi – Chiều dài

b) Diện tích thửa rộng = chiều dài x chiều rộng

Số tạ thóc thu được = diện tích thửa ruộng : 100 x 70

Lời giải chi tiết:

a)                                                             Nửa chu vi thửa ruộng là:

180 : 2 = 90 (m)

Ta có sơ đồ:

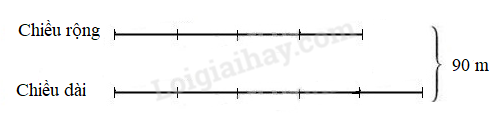
Tổng số phần bằng nhau là:

5 + 4 = 9 (phần)

Chiều dài thửa ruộng đó là:

90 : 9 x 5 = 50 (m)

Chiều rộng thửa ruộng đó là:

90 – 50 = 40 (m)

b)                                                         Diện tích thửa ruộng đó là:

50 x 40 = 2000 (m ² )

Trên cả thửa ruộng đó người ta thu hoạch được số tạ thóc là:

2000 : 100 x 70 = 1400 (kg)

Đổi 1400kg = 14 tạ

Đáp số: a) Chiều dài: 50m; chiều rộng: 40m

b) 14 tạ thóc

Câu 11

Một mảnh vườn hình chữ nhật có chu vi bằng chu vi của mảnh vườn hình vuông có cạnh 49m, chiều rộng của mảnh vườn hình chữ nhật bằng $\frac{2}{5}$chiều dài.

a) Tính diện tích của mảnh vườn hình chữ nhật.

b) Người ta dùng $\frac{1}{{40}}$diện tích của mảnh vườn để làm lối đi, phần còn lại trồng cây ăn quả. Tính diện tích phần đất trồng cây ăn quả.

Phương pháp giải:

a) Chu vi vườn hình vuông = Độ dìa cạnh x 4

Nửa chu vi vườn hình chữ nhật = chu vi hình vuông : 2

Tìm tổng số phần bằng nhau

Chiều dài = nửa chu vi hình chữ nhật : tổng số phần bằng nhau x 5

Chiều rộng = nửa chu vi hình chữ nhật – chiều dài

Diện tích hình chữ nhật =  Chiều dài x chiều rộng

b) Diện tích để làm lối đi = diện tích hình chữ nhật : 40

Diện tích để trồng cây ăn quả = diện tích hình chữ nhật – diện tích để làm lối đi

Lời giải chi tiết:

a)                                                               Chu vi hình vuông là:

49 × 4 = 196 (m)

Chu vi hình chữ nhật bằng chu vi hình vuông là 196m

Nửa chu vi hình chữ nhật là:

196 : 2 = 98 ( m )

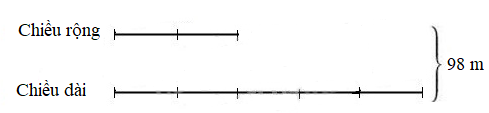
Tổng số phần bằng nhau là:

2 + 5 = 7 (phần)

Chiều dài của hình chữ nhật là:

98 : 7 x 5 = 70 (m)

Chiều rộng của hình chữ nhật là:

98 – 70 = 28 (m)

Diện tích hình chữ nhật là:

70 x 28 = 1960 (m ² )

b)                                                            Diện tích để làm lối đi là:

1960 : 40 = 49 ( m ² )

Diện tích để trồng cây ăn quả là:

1960 – 49 = 1911 (m ² )

Đáp số: a) 1960 m ²

b) 1911m ²

Câu 12

Viết các phân số sau theo thứ tự từ lớn đến bé:

$\frac{{43}}{{24}};\frac{{43}}{{21}};\frac{{2019}}{{2019}};\frac{{2010}}{{2018}};\frac{{2010}}{{2019}}$

Phương pháp giải:

- Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn

- Phân số có tử số bé hơn hơn mẫu số thì phân số đó bé hơn 1

- Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1

- Phân số có tử số bằng mẫu số thì phân số đó bằng 1

Lời giải chi tiết:

Ta có: $\frac{{2019}}{{2019}} = 1$                                               (1)

+ Hai phân số $\frac{{43}}{{24}};\frac{{43}}{{21}}$ đều lớn hơn 1

Mà 21 < 24 nên $\frac{{43}}{{21}} > \frac{{43}}{{24}}$                                (2)

+ Hai phân số $\frac{{2010}}{{2018}};\frac{{2010}}{{2019}}$ đều bé hơn 1

Mà 2018 < 2019 ó $\frac{{2010}}{{2018}} > \frac{{2010}}{{2019}}$                   (3)

Từ (1); (2); (3) Suy ra $\frac{{43}}{{21}} > \frac{{43}}{{24}} > \frac{{2019}}{{2019}} > \frac{{2010}}{{2018}} > \frac{{2010}}{{2019}}$

Vậy các phân số theo thứ tự từ lớn đến bé là: $\frac{{43}}{{21}};\frac{{43}}{{24}};\frac{{2019}}{{2019}};\frac{{2010}}{{2018}};\frac{{2010}}{{2019}}$