Giải Toán 5 Bài 74. Ôn tập một số yếu tố thống kê và xác suất - Kết nối tri thức với cuộc sống — Không quảng cáo

Luyện tập 1 Câu 1

Trả lời câu hỏi 1 trang 123 SGK Toán 5 Kết nối tri thức

Nam, Việt và Mai cắt giấy được một số hình phẳng đã học rồi tô màu các hình đó. Rô-bốt phân loại và sắp xếp các hình đó theo màu đỏ, vàng, xanh như biểu đồ dưới đây.

BIỂU ĐỒ VỀ CÁC MÀU ĐỎ, VÀNG, XANH CỦA CÁC HÌNH

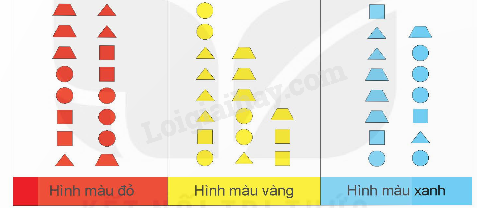
Quan sát biểu đồ và hoàn thành các bảng sau:

a) Xếp loại theo các màu:

b) Xếp loại theo hình dạng:

c) Xếp loại theo hình dạng và màu:

Phương pháp giải:

Quan sát biểu đồ rồi điền số thích hợp vào ô trống.

Lời giải chi tiết:

a)

b)

c)

Luyện tập 1 Câu 2

Trả lời câu hỏi 2 trang 124 SGK Toán 5 Kết nối tri thức

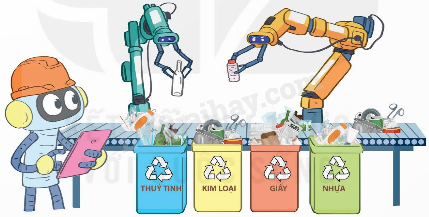
Ở một nhà máy tái chế rác thải, Rô-bốt có tham gia vào khâu phân loại rác. Khi rác thải chạy qua một băng chuyền, Rô-bốt đã nhặt phân loại: loại A là rác thủy tinh; loại B là rác kim loại; loại C là rác giấy; loại D là rác nhựa (như hình vẽ).

Người ta đã cho 1 tấn rác thải chạy qua băng chuyền. Từ số rác thải đó, Rô-bốt đã phân loại được 95 kg rác thủy tinh (A); 150 kg rác kim loại (B); 105 kg rác giấy (C); 120 kg rác nhựa (D).

a) Số?

Trong 1 tấn rác thải qua băng chuyền:

b) Sắp xếp số ki-lô-gam rác mỗi loại A, B, C, D theo thứ tự từ lớn đến bé.

Phương pháp giải:

a) Dựa vào số liệu đã cho ở đề bài, em điền số thích hợp vào ô trống.

b) So sánh cân nặng ở mỗi loại rác rồi sắp xếp thứ tự từ lớn đến bé.

Lời giải chi tiết:

a)

b)

Vì 150 > 120 > 105 > 95 nên ta sắp xếp số ki-lô-gam rác mỗi loại theo thứ tự từ lớn đến bé là:

Loại B; loại D; loại C; loại A.

Luyện tập 1 Câu 3

Trả lời câu hỏi 3 trang 124 SGK Toán 5 Kết nối tri thức

Theo quy hoạch của Bộ Nông Nghiệp và Phát triển nông thôn, đến năm 2020, bốn tỉnh Tây Nguyên: Đắk Lắk, Lâm Đồng, Đắk Nông, Gia Lai được xác định là vùng trọng điểm cà phê của cả nước ổn định với tổng diện tích 530 000 ha, trong đó Đắk Lắk là 190 000 ha, Lâm Đồng là 150 000 ha, Đắk Nông là 115 000 ha, còn lại là của Gia Lai (theo https://mard.gov.vn).

a) Số?

b) Dưới đây là biểu đồ về diện tích trồng cà phê của bốn tỉnh Tây Nguyên

DIỆN TÍCH TRỒNG CÀ PHÊ CỦA BỐN TỈNH TÂY NGUYÊN

Quan sát biểu đồ rồi trả lời câu hỏi:

- Diện tích trồng cà phê ở tỉnh nào nhiều nhất, tỉnh nào ít nhất?

- Trung bình mỗi tỉnh trồng bao nhiêu héc-ta cà phê?

Phương pháp giải:

a) Dựa vào số liệu đề bài cho, em hãy điền số thích hợp vào ô trống.

b) Quan sát biểu đồ rồi trả lời câu hỏi.

Lời giải chi tiết:

a)

b)

- Diện tích trồng cà phê ở tỉnh Đắk Lắk nhiều nhất, tỉnh Gia Lai ít nhất.

- Trung bình mỗi tỉnh trồng số héc-ta cà phê là:

(75 + 115 + 190 + 150) : 4 = 132,5 (héc-ta)

Luyện tập 1 Câu 4

Trả lời câu hỏi 4 trang 125 SGK Toán 5 Kết nối tri thức

Một trận bóng đá của giải Vô địch Quốc gia Việt Nam có 20 000 khán giả, trong đó khán đài A có 6 000 khán giả, khán đài B có 8 000 khán giả, khán đài C có 3 600 khán giả, còn lại ở khán đài D.

a) Hoàn thành bảng sau

b) Tìm tỉ số phần trăm của số khán giả ở mỗi khán đài và số khán giả xem trận đấu.

c) Rô-bốt đã vẽ biểu đồ về tỉ số phần trăm số khán giả ở mỗi khán đài và số khán giả xem trận đấu, nhưng chưa ghi tỉ số phần trăm vào mỗi phần hình quạt. Em hãy hoàn thành biểu đồ hình quạt tròn đó.

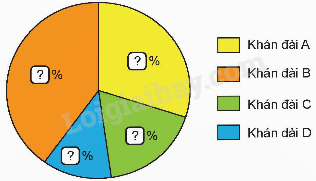
Phương pháp giải:

a) Dựa vào số liệu đề bài cho, em hãy điền số thích hợp vào ô trống.

b) Tỉ số phần trăm của số khán giả ở mỗi khán đài và số khán giả xem trận đấu = số lượng khán giả ở mỗi khán đài : số khán giả xem trận đấu x 100%.

c) Dựa vào kết quả câu b để hoàn thành biểu đồ.

Lời giải chi tiết:

a)

b)

- Tỉ số phần trăm của số khán giả ở khán đài Avà số khán giả xem trận đấu là:

6 000 : 20 000 x 100% = 30%

- Tỉ số phần trăm của số khán giả ở khán đài B và số khán giả xem trận đấu là:

8 000 : 20 000 x 100% = 40%

- Tỉ số phần trăm của số khán giả ở khán đài C và số khán giả xem trận đấu là:

3 600 : 20 000 x 100% = 18%

- Tỉ số phần trăm của số khán giả ở khán đài D và số khán giả xem trận đấu là:

100% - 30% - 40% - 18% = 12%

c)

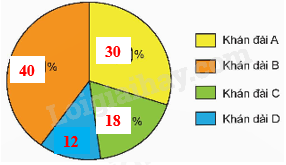
Luyện tập 2 Câu 1

Trả lời câu hỏi 1 trang 126 SGK Toán 5 Kết nối tri thức

Chọn đáp án đúng.

Gieo hai xúc xắc. Chọn khả năng xảy ra trong mỗi trường hợp sau:

a) Tổng số chấm ở hai mặt trên của hai xúc xắc là số chẵn.

A. Chắc chắn

B. Có thể

C. Không thể

b) Tổng số chấm ở hai mặt trên của hai xúc xắc là 13.

A. Chắc chắn

B. Có thể

C. Không thể

c) Tổng số chấm ở hai mặt trên của hai xúc xắc là số bé hơn 13 và lớn hơn 1.

A. Chắc chắn

B. Có thể

C. Không thể

Phương pháp giải:

Chọn đáp án đúng.

Lời giải chi tiết:

a) Chọn đáp án B.

b) Chọn đáp án C.

c) Chọn đáp án A.

Luyện tập 2 Câu 2

Trả lời câu hỏi 2 trang 126 SGK Toán 5 Kết nối tri thức

Trong hộp có 2 quả bóng đỏ và 3 quả bóng xanh. Nếu Rô-bốt lấy ra từ trong hộp cùng một lúc 3 quả bóng thì có các khả năng nào về màu của 3 quả bóng đó có thể xảy ra?

Phương pháp giải:

Liệt kê các khả năng về màu của 3 quả bóng.

Lời giải chi tiết:

Các khả năng về màu của 3 quả bóng có thể xảy ra là:

Đỏ, xanh, xanh

Đỏ, đỏ, xanh

Xanh, xanh, xanh

Luyện tập 2 Câu 3

Trả lời câu hỏi 3 trang 127 SGK Toán 5 Kết nối tri thức

Việt gieo xúc xắc nhiều lần rồi ghi lại kết quả nhận được như bảng sau (chẳng hạn, mặt 6 chấm xuất hiện 4 lần ghi |||| ).

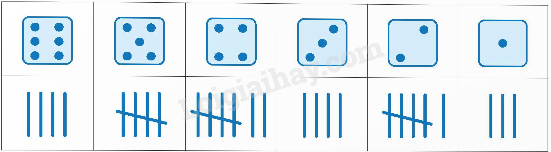
a) Chọn câu trả lời đúng.

Mặt 5 chấm đã xuất hiện bao nhiêu lần?

A. 7 lần

B. 6 lần

C. 5 lần

D. 4 lần

b) Mặt nào xuất hiện nhiều lần nhất, mặt nào xuất hiện ít lần nhất?

c) Hai mặt nào có số lần xuất hiện bằng nhau?

Phương pháp giải:

Quan sát bảng ghi rồi trả lời câu hỏi.

Lời giải chi tiết:

a) Chọn đáp án C .

b) Mặt 4 chấm xuất hiện nhiều lần nhất, mặt 1 chấm xuất hiện ít lần nhất.

c) Mặt 6 chấm và mặt 3 chấm có số lần xuất hiện bằng nhau.

Luyện tập 2 Câu 4

Trả lời câu hỏi 4 trang 127 SGK Toán 5 Kết nối tri thức

Mai gieo đồng thời hai đồng xu 25 lần, đếm số lần lặp lại của khả năng hai đồng xu xuất hiện cùng mặt sấp, hoặc xuất hiện cùng mặt ngửa hoặc xuất hiện một mặt sấp, một mặt ngửa rồi ghi lại kết quả nhận được như bảng sau:

a) Số lần lặp lại khả năng xuất hiện hai mặt đồng xu ở dạng nào nhiều nhất, ở dạng nào ít nhất?

b) Tìm tỉ số của số lần lặp lại của mỗi khả năng xuất hiện so với tổng số lần gieo hai đồng xu.

Phương pháp giải:

Quan sát bảng ghi rồi trả lời câu hỏi.

Lời giải chi tiết:

a) Số lần lặp lại khả năng xuất hiện hai mặt đồng xu ở dạng “Một mặt sấp, một mặt ngửa” là nhiều nhất, ở dạng “Hai mặt ngửa” là ít nhất.

b) Tỉ số của số lần lặp lại của khả năng “Hai mặt sấp” với tổng số lần gieo hai đồng xu là: $\frac{8}{{25}}.$

Tỉ số của số lần lặp lại của khả năng “Hai mặt ngửa” với tổng số lần gieo hai đồng xu là: $\frac{7}{{25}}.$

Tỉ số của số lần lặp lại của khả năng “Một mặt sấp, một mặt ngửa” với tổng số lần gieo hai đồng xu là: $\frac{{10}}{{25}}.$