Giải Toán 5 Bài 75. Ôn tập chung - Kết nối tri thức với cuộc sống — Không quảng cáo

Luyện tập 1 Câu 1

Trả lời câu hỏi 1 trang 128 SGK Toán 5 Kết nối tri thức

a) Hoàn thành bảng sau.

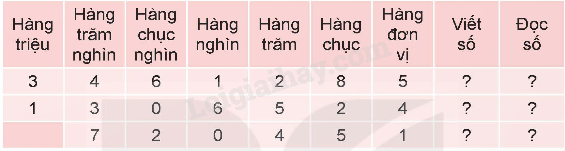
b) Nêu giá trị của chữ số 2 trong mỗi số viết ở câu a.

Phương pháp giải:

a) Đọc số tự nhiên: Đọc số theo các lớp, từ trái sang phải: Với mỗi lớp, ta đọc như đọc các số có một, hai hoặc ba chữ số rồi kèm theo tên lớp.

Chú ý: Để cho gọn, ta có thể không đọc tên lớp đơn vị.

b) Xác định vị trí của chữ số 2 trong mỗi số đó rồi ghi giá trị tương ứng của chữ số đó.

Lời giải chi tiết:

a)

b) Xác định vị trí của chữ số 2 trong mỗi số đó rồi ghi giá trị tương ứng của chữ số đó.

Chữ số 2 trong số 3 461 285 có giá trị là 200

Chữ số 2 trong số 1 306 524 có giá trị là 20

Chữ số 2 trong số 720 451 có giá trị là 20 000

Luyện tập 1 Câu 2

Trả lời câu hỏi 2 trang 128 SGK Toán 5 Kết nối tri thức

Sắp xếp các số 67 245, 67 425, 67 524, 65 742 theo thứ tự từ bé đến lớn.

Phương pháp giải:

So sánh các số rồi sắp xếp theo thứ tự từ bé đến lớn.

Lời giải chi tiết:

Ta có: 65 742 < 67 245 < 67 425 < 67 524 nên ta sắp xếp các số theo thứ tự từ bé đến lớn như sau: 65 742; 67 245; 67 425; 67 524.

Luyện tập 1 Câu 3

Trả lời câu hỏi 3 trang 128 SGK Toán 5 Kết nối tri thức

Chọn câu trả lời đúng.

a) Đã tô màu $\frac{5}{8}$ hình nào dưới đây?

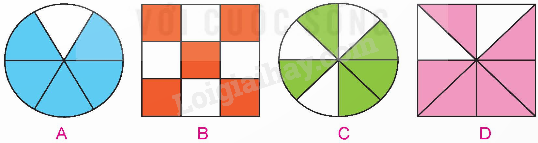
b) $\frac{2}{3}$ là phân số rút gọn của phân số nào dưới đây?

A. $\frac{4}{8}$

B. $\frac{6}{{18}}$

C. $\frac{{16}}{{24}}$

D. $\frac{8}{9}$

Phương pháp giải:

a) Quan sát hình vẽ rồi chọn đáp án đúng.

b) Rút gọn phân số ở từng đáp án rồi chọn đáp án đúng.

Lời giải chi tiết:

a) Chọn đáp án C.

b) Chọn đáp án C.

Luyện tập 1 Câu 4

Trả lời câu hỏi 4 trang 129 SGK Toán 5 Kết nối tri thức

a) Số?

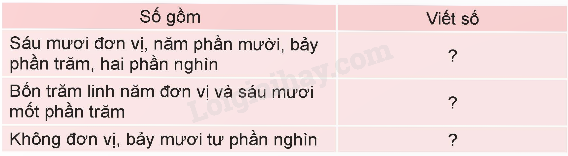
b) Tìm số thập phân thích hợp rồi đọc số thập phân đó.

5 m 8 dm = ? m

74 cm = ? m

425 g = ? kg

85 ml = ? l

Phương pháp giải:

a) Điền số thích hợp vào ô trống.

b) Dùng kiến thức về đơn vị đo độ dài để điền số thích hợp vào ô trống.

Lời giải chi tiết:

a)

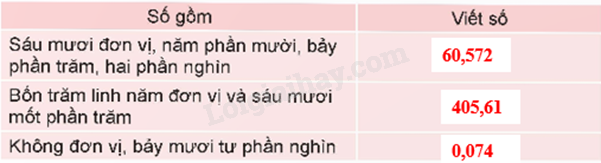
b)

5 m 8 dm = 5,8 m

74 cm = 0,74 m

425 g = 0,425 kg

85 ml = 0,085 l

Luyện tập 1 Câu 5

Trả lời câu hỏi 5 trang 129 SGK Toán 5 Kết nối tri thức

a) Sắp xếp các số 70,571; 70,517; 71,057; 70,715 theo thứ tự từ lớn đến bé.

b) Chọn câu trả lời đúng.

Ba rô-bốt vàng, đỏ, xanh có chiều cao là một trong các số đo: 98 cm; 0,89 m; 1,02 m. Biết rô-bốt vàng cao hơn rô-bốt đỏ nhưng thấp hơn rô-bốt xanh.

Chiều cao của rô-bốt đỏ là:

A. 98 cm

B. 0,89 m

C. 1,02 m

Chiều cao của rô-bốt xanh là:

A. 98 cm

B. 0,89 m

C. 1,02 m

Phương pháp giải:

a) So sánh các số thập phân rồi sắp xếp theo thứ tự từ lớn đến bé.

b) Dựa vào dữ liệu đề bài cho để chọn đáp án đúng.

Lời giải chi tiết:

a) Ta có: 71,057 > 70,715 > 70,571 > 70,517 nên ta sắp xếp các số theo thứ tự từ lớn đến bé là:

71,057; 70,715; 70,571; 70,517

b) Chiều cao của rô-bốt đỏ là: Đáp án B . 0,89 m

Chiều cao của rô-bốt xanh là: Đáp án C .1,02 m

Luyện tập 2 Câu 1

Trả lời câu hỏi 1 trang 130 SGK Toán 5 Kết nối tri thức

Đặt tính rồi tính.

a) 2 564 + 3 819

b) 62 835 – 24 173

c) 342 x 14

d) 2 625 : 15

Phương pháp giải:

- Thực hiện đặt tính

- Với phép cộng, phép trừ: Cộng hoặc trừ các chữ số cùng hàng thẳng cột lần lượt từ phải sang trái.

- Với phép nhân: Thực hiện nhân 2 với từng chữ số của số vừa viết theo thứ tự từ phải sang trái.

- Với phép chia: Thực hiện chia lần lượt từ trái sang phải

Lời giải chi tiết:

Luyện tập 2 Câu 2

Trả lời câu hỏi 2 trang 130 SGK Toán 5 Kết nối tri thức

Đặt tính rồi tính.

a) 148,32 + 270,84

b) 197,25 – 92,73

c) 34,6 x 5,7

d) 28,8 : 4,5

Phương pháp giải:

Muốn cộng hai số thập phân, ta làm như sau:

- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Cộng như cộng hai số tự nhiên.

- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.

Muốn trừ hai số thập phân, ta làm như sau:

- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Trừ như trừ hai số tự nhiên.

- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.

Muốn nhân một số thập phân với một số thập phân, ta làm như sau:

- Đặt tính giống như nhân hai số tự nhiên.

- Thực hiện nhân như nhân hai số tự nhiên.

- Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.

Muốn chia một số thập phân cho một số thập phân, ta làm như sau:

- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.

- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia cho số tự nhiên.

Lời giải chi tiết:

Luyện tập 2 Câu 3

Trả lời câu hỏi 3 trang 130 SGK Toán 5 Kết nối tri thức

Tính giá trị của biểu thức.

a) 2 354 + 1 736 : 4

b) 21,4 x (37,8 – 32,5)

c) $\frac{5}{6} - \frac{2}{3} - \frac{2}{5}$

Phương pháp giải:

- Khi tính giá trị của các biểu thức có dấu ngoặc () thì trước tiên ta thực hiện các phép tính trong ngoặc.

- Nếu trong biểu thức chỉ có các phép tính cộng, trừ, nhân, chia thì ta thực hiện các phép tính nhân, chia trước; rồi thực hiện các phép tính cộng, trừ sau.

- Biểu thức chỉ có phép cộng và phép trừ thì tính lần lượt từ trái sang phải.

Lời giải chi tiết:

a) 2 354 + 1 736 : 4

= 2 354 + 434

= 2 788

b) 21,4 x (37,8 – 32,5)

= 21,4 x 5,3

= 113,42

c) $\frac{5}{6} - \frac{2}{3} + \frac{2}{5} = \frac{{25}}{{30}} - \frac{{20}}{{30}} + \frac{{12}}{{30}} = \frac{{17}}{{30}}.$

Luyện tập 2 Câu 4

Trả lời câu hỏi 4 trang 130 SGK Toán 5 Kết nối tri thức

Tính bằng cách thuận tiện.

a) 137 x 25 + 137 x 75

b) $\left( {\frac{4}{9} + \frac{3}{5}} \right) + \frac{5}{9}$

c) $124,46 + 98,31 + 75,54$

Phương pháp giải:

a) Sử dụng tính chất phân phối của phép nhân và phép cộng.

b) Sử dụng tính chất kết hợp, giao hoán để nhóm các phân số có cùng mẫu số vào với nhau.

c) Sử dụng tính chất kết hợp, giao hoán để nhóm các số thập phân có tổng là các số tròn chục, tròn trăm, tròn nghìn,...

Lời giải chi tiết:

a) 137 x 25 + 137 x 75

= 137 x (25 + 75)

= 137 x 100

= 13 700

b) $\left( {\frac{4}{9} + \frac{3}{5}} \right) + \frac{5}{9}$

$ = \left( {\frac{4}{9} + \frac{5}{9}} \right) + \frac{3}{5}$

$ = 1 + \frac{3}{5}$

$ = \frac{8}{5}$

c) $124,46 + 98,31 + 75,54$

= (124,46 + 75,54) + 98,31

= 200 + 98,31

= 298,31

Luyện tập 2 Câu 5

Trả lời câu hỏi 5 trang 130 SGK Toán 5 Kết nối tri thức

Tính.

a) 14 giờ 36 phút + 5 giờ 15 phút

b) 10 giờ 15 phút – 6 giờ 30 phút

c) 4,5 giờ x 3

d) 38,5 phút : 5

Phương pháp giải:

a)

- Đặt tính thẳng hàng và thực hiện tính như đối với phép cộng các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số đo thời gian ở đơn vị bé có thể chuyển đổi sang đơn vị lớn thì ta thực hiện chuyển đổi sang đơn vị lớn hơn.

b)

- Đặt tính thẳng hàng và thực hiện tính như đối với phép trừ các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số đo theo đơn vị nào đó ở số bị trừ bé hơn số đo tương ứng ở số trừ thì cần chuyển đổi 1 đơn vị hàng lớn hơn liền kề sang đơn vị nhỏ hơn rồi thực hiện phép trừ như bình thường.

c)

- Đặt tính thẳng hàng và thực hiện tính như đối với phép nhân các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số đo thời gian ở đơn vị bé có thể chuyển đổi sang đơn vị lớn thì ta thực hiện chuyển đổi sang đơn vị lớn hơn.

d)

- Ta đặt tính như đối với phép chia các số tự nhiên.

- Chia từng số đo ở số bị chia cho số chia (theo thứ tự từ trái sang phải).

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

Lời giải chi tiết:

a) 14 giờ 36 phút + 5 giờ 15 phút = 19 giờ 51 phút

b) 10 giờ 15 phút – 6 giờ 30 phút = 3 giờ 45 phút

c) 4,5 giờ x 3 = 13,5 giờ

d) 38,5 phút : 5 = 7,7 giờ

Luyện tập 3 Câu 1

Trả lời câu hỏi 1 trang 130 SGK Toán 5 Kết nối tri thức

Chọn câu trả lời đúng.

a) Số thập phân thích hợp viết vào chỗ chấm của 75 m = … km là:

A. 7,5

B. 0,75

C. 0,075

D. 0,0075

b) Số thập phân thích hợp viết vào chỗ chấm của 2 kg 45 g = … kg là:

A. 245

B. 2,45

C. 2,045

D. 0,245

c) Số thập phân thích hợp viết vào chỗ chấm của 652 ml = … l là:

A. 6,52

B. 0,652

C. 0,0652

D. 652

Phương pháp giải:

Dựa vào lý thuyết về các đơn vị đo độ dài và đo khối lượng đã học.

Lời giải chi tiết:

a) Chọn đáp án C .

b) Chọn đáp án C .

c) Chọn đáp án B .

Luyện tập 3 Câu 2

Trả lời câu hỏi 2 trang 131 SGK Toán 5 Kết nối tri thức

Chọn câu trả lời đúng.

a) Trong 20 hộp sữa chua có 12 hộp là loại sữa chua không đường, còn lại là loại sữa chua có đường. Tỉ số phần trăm của số hộp sữa chua có đường và tổng số hộp sữa chua là:

A. 8%

B. 20%

C. 4%

D. 40%

b) Lãi suất tiết kiệm là 0,5%/tháng. Bác Tư gửi tiết kiệm 10 000 000 đồng thì sau 1 tháng nhận được cả tiền gửi và tiền lãi là:

A. 150 000 đồng

B. 1 050 000 đồng

C. 10 050 000 đồng

D. 1 500 000 đồng

Phương pháp giải:

a)

- Số hộp sữa chua có đường = Tổng số hộp sữa chua – số hộp sữa chua không đường.

- Tỉ số phần trăm của số hộp sữa chua có đường và tổng số hộp sữa chua = số hộp sữa chua có đường : tổng số hộp sữa chua x 100%.

b)

- Số tiền lãi sau 1 tháng = Số tiền gửi tiết kiệm x lãi suất hàng tháng.

- Số tiền nhận được sau 1 tháng = Số tiền gửi tiết kiệm + số tiền lãi sau 1 tháng.

Lời giải chi tiết:

a)

Số hộp sữa chua có đường là:

20 – 12 = 8 (hộp)

Tỉ số phần trăm của số hộp sữa chua có đường và tổng số hộp sữa chua là:

8 : 20 x 100% = 40%

Chọn đáp án D .

b)

Số tiền lãi sau 1 tháng là:

10 000 000 x 0,5% = 50 000 (đồng)

Số tiền nhận được sau 1 tháng là:

10 000 000 + 50 000 = 10 050 000 (đồng)

Chọn đáp án C .

Luyện tập 3 Câu 3

Trả lời câu hỏi 3 trang 131 SGK Toán 5 Kết nối tri thức

Nam cắt giấy màu được 3 hình có kích thước như hình dưới đây.

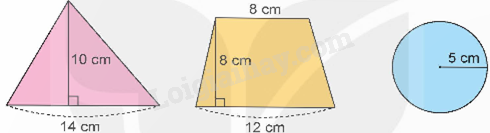
a) Chọn câu trả lời đúng.

Trong các hình trên, hình có diện tích lớn nhất là:

A. Hình tam giác

B. Hình thang

C. Hình tròn

b) Số?

Chu vi hình tròn là ? cm

Phương pháp giải:

a) Tính diện tích mỗi hình và so sánh.

b) Chu vi hình tròn = 3,14 x bán kính x 2.

Lời giải chi tiết:

a)

Diện tích tam giác là:

(10 x 14) : 2 = 70 (cm ² )

Diện tích hình thang là:

(12 + 8) x 8 : 2 = 80 (cm ² )

Diện tích hình tròn là:

3,14 x 5 x 5 = 78,5 (cm ² )

Ta có 80 > 78,5 > 70 nên hình thang có diện tích lớn nhất.

Chọn đáp án B.

b) Chu vi hình tròn là:

3,14 x 5 x 2 = 31,4 (cm)

Luyện tập 3 Câu 4

Trả lời câu hỏi 4 trang 131 SGK Toán 5 Kết nối tri thức

Cho khối gỗ hình lập phương M và khối gỗ hình hộp chữ nhật N có kích thước như hình dưới đây.

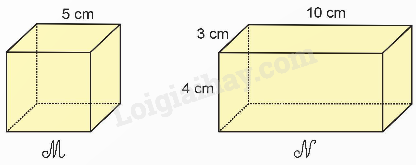
a) Số?

Diện tích xung quanh hình lập phương M là ? cm ² .

Diện tích xung quanh hình hộp chữ nhật N là ? cm ² .

Diện tích toàn phần hình lập phương M là ? cm ² .

Diện tích toàn phần hình hộp chữ nhật N là ? cm ² .

b) Thể tích hình nào lớn hơn và lớn hơn bao nhiêu xăng-ti-mét khối?

Phương pháp giải:

a)

- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.

- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.

- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

b)

- Thể tích hình lập phương = cạnh x cạnh x cạnh.

- Thể tích hình hộp chữ nhật = chiều dài x chiều rộng x chiều cao.

Lời giải chi tiết:

a)

Diện tích xung quanh hình lập phương M là:

5 x 5 x 4 = 100 (cm ² )

Diện tích xung quanh hình hộp chữ nhật N là:

(10 + 3) x 2 x 4 = 104 (cm ² )

Diện tích toàn phần hình lập phương M là:

5 x 5 x 6 = 150 (cm ² )

Diện tích toàn phần hình lập phương N là:

150 + 10 x 3 x 2 = 210 (cm ² )

Diện tích xung quanh hình lập phương M là 100 cm ² .

Diện tích xung quanh hình hộp chữ nhật Nlà 104 cm ² .

Diện tích toàn phần hình lập phương M là 150 cm ² .

Diện tích toàn phần hình lập phương N là 210 cm ² .

b)

Thể tích hình lập phương là:

5 x 5 x 5 = 125 (cm ³ )

Thể tích hình hộp chữ nhật là:

10 x 3 x 4 = 120 (cm ³ )

Vì 125 > 120 nên thể tích hình lập phương lớn hơn và lớn hơn 125 – 120 = 5 cm ³ .

Luyện tập 3 Câu 5

Trả lời câu hỏi 5 trang 132 SGK Toán 5 Kết nối tri thức

Tìm số tự nhiên hoặc số thập phân thích hợp.

Phương pháp giải:

- Quãng đường = vận tốc x thời gian.

- Thời gian = quãng đường : vận tốc.

- Vận tốc = quãng đường : thời gian.

Lời giải chi tiết:

- Đại bàng: t = 96 : 24 = 4 giờ

- Báo: Đổi 24 phút = 0,4 giờ

s = 120 x 0,4 = 48 km

- Đà điểu: Đổi 5,250 km = 5 250 m

v = 5 250 : 300 = 17,5 m/s

Luyện tập 4 Câu 1

Trả lời câu hỏi 1 trang 132 SGK Toán 5 Kết nối tri thức

Thống kê số huy chương vàng (HCV), huy chương bạc (HCB), huy chương đồng (HCĐ) bốn môn Vật, Bơi, Lặn, Wushu của Đoàn Việt Nam tại Sea Games 31, ta có bảng sau (theo https://tuoitre.vn năm 2022).

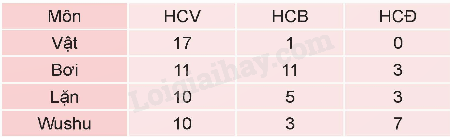
b) Biểu đồ dưới đây cho biết số HCV bốn môn Vật, Wushu, Lặn, Bơi của Đoàn Việt Nam tại Sea Games 31.

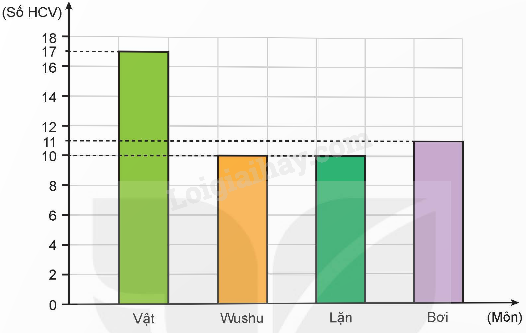
Quan sát biểu đồ rồi trả lời các câu hỏi.

• Môn nào có nhiều HCV nhất?
• Hai môn nào có số HCV bằng nhau?
• Trung bình mỗi môn có bao nhiêu HCV?

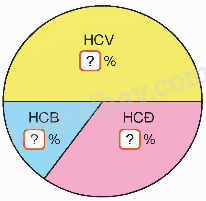
b) Rô-bốt đã vẽ biểu đồ hình quạt tròn bên cho biết tỉ số phần trăm số HCV, HCB, HCĐ so với tổng số huy chương đạt được của môn Wushu nhưng chưa ghi tỉ số phần trăm của mỗi môn vào biểu đồ.

Dựa vào bảng thống kê, tìm tỉ số phần trăm của số HCV, HCB, HCĐ và tổng số huy chương ở môn Wushu, rồi hoàn thành biểu đồ hình quạt tròn đó.

So sánh tỉ số phần trăm của số HCV với tổng số phần trăm của số HCB và HCĐ ở môn Wushu.

Phương pháp giải:

a) Quan sát biểu đồ rồi trả lời câu hỏi

b) Điền số thích hợp vào ô trống.

Lời giải chi tiết:

a)

Môn Vật có nhiều HCV nhất

Môn Wushu và môn Lặn có số HCV bằng nhau.

Trung bình mỗi môn có số HCV là: (17 + 10 + 10 + 11) : 4 = 12 (HCV)

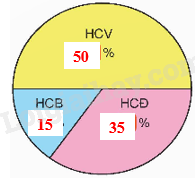
b)

Tỉ số phần trăm của số HCV và tổng số huy chương ở môn Wushu là:

10 : 20 x 100% = 50%

Tỉ số phần trăm của số HCB và tổng số huy chương ở môn Wushu là:

3 : 20 x 100% = 15%

Tỉ số phần trăm của số HCĐ và tổng số huy chương ở môn Wushu là:

7 : 20 x 100% = 35%

Luyện tập 4 Câu 2

Trả lời câu hỏi 2 trang 134 SGK Toán 5 Kết nối tri thức

Một bể cá dạng hình hộp chữ nhật có chu vi đáy là 320 m, chiều rộng của đáy bằng $\frac{3}{5}$ chiều dài cảu đáy, chiều cao bể cá là 50 cm.

a) Tính chiều dài và chiều rộng đáy bể cá.

b) Biết mực nước ở bể cá là 40 cm. Hỏi lượng nước hiện có trong bể chiếm bao nhiêu phần trăm so với lượng nước khi đầy bể?

Phương pháp giải:

a)

1. Vẽ sơ đồ: coi chiều rộng (đóng vai trò số bé) gồm 3 phần bằng nhau thì chiều dài (đóng vai trò số lớn) gồm 5 phần như thế.

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

5. Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn).

Chú ý: Có thể làm gộp bước 2 và bước 3

b)

- Thể tích bể cá = chiều dài x chiều rộng x chiều cao.

- Thể tích nước trong bể cá = chiều dài x chiều rộng x chiều cao mực nước.

- Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể = thể tích nước trong bể cá : thể tích bể cá x 100%.

Lời giải chi tiết:

a) Tổng chiều dài và chiều rộng là:

320 : 2 = 160 (m)

Ta có sơ đồ:

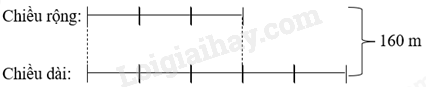
Theo sơ đồ, giá trị mỗi phần bằng nhau là:

160 : (3 + 5) = 20 (m)

Chiều rộng là:

20 x 3 = 60 (m)

Chiều dài là

20 x 5 = 100 (m)

b) Thể tích bể cá là:

100 x 60 x 50 = 300 000 (m ³ )

Thể tích nước trong bể cá là:

100 x 60 x 40 = 240 000 (m ³ )

Tỉ số phần trăm của lượng nước hiện có trong bể với lượng nước khi đầy bể là:

240 000 : 300 000 = 80%

Đáp số: a) Chiều rộng: 60 m; Chiều dài: 100 m.

b) 80%.

Luyện tập 4 Câu 3

Trả lời câu hỏi 3 trang 134 SGK Toán 5 Kết nối tri thức

Cùng xuất phát ở bến A đi đến khu du lịch B, Việt đi xe buýt thì đến nơi lúc 9 giờ, Mai đi xe taxi đến nơi lúc 8 giờ 15 phút. Rô-bốt cho biết cùng trên quãng đường AB, thời gian đi của taxi bằng $\frac{2}{3}$ thời gian đi của xe buýt.

a) Tính thời gian của mỗi xe ô tô đi trên quãng đường AB.

b) Tính độ dài quãng đường AB, biết vận tốc của xe taxi là 60 km/h.

Phương pháp giải:

a)

1. Vẽ sơ đồ: coi thời gian đi của taxi (đóng vai trò số bé) gồm 2 phần bằng nhau thì thời gian của xe buýt (đóng vai trò số lớn) gồm 3 phần bằng nhau như thế.

2. Tìm hiệu số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.

4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

5. Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn).

Chú ý: Có thể làm gộp bước 2 và bước 3

b)

Quãng đường = vận tốc x thời gian.

Lời giải chi tiết:

a) Đổi 8 giờ 15 phút = 8,25 giờ

Thời gian đi của xe buýt dài hơn thời gian đi của taxi là:

9 – 8,25 = 0,75 (giờ)

Ta có sơ đồ:

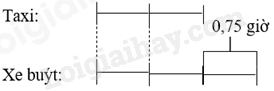
Theo sơ đồ, giá trị mỗi phần bằng nhau là:

0,75 : (3 – 2) = 0,75 (giờ)

Thời gian đi xe taxi là:

0,75 x 2 = 1,5 (giờ)

Thời gian đi xe buýt là:

0,75 x 3 = 2,25 (giờ)

b) Độ dài quãng đường AB là:

60 x 1,5 = 90 (km)

Đáp số: a) 1,5 giờ; 2,25 giờ

b) 90 km.

Luyện tập 4 Câu 4

Trả lời câu hỏi 4 trang 134 SGK Toán 5 Kết nối tri thức

Một tỉnh miền núi có diện tích khoảng 10 000 km ² . Mật độ dân số ở tỉnh đó khoảng 80 người/km ² (nghĩa là cứ mỗi ki-lô-mét vuông có trung bình 80 người). Nếu muốn tăng mật độ dân số của tỉnh đó là 90 người/km ² thì số dân của tỉnh phải tăng thêm bao nhiêu người?

Phương pháp giải:

- Số dân của tỉnh với mật độ 80 người/km ² = diện tích tỉnh x mật độ dân số.

- Số dân của tỉnh với mật độ 90 người/km ² = diện tích tỉnh x mật độ dân số.

- Số dân của tỉnh phải tăng lên để mật độ dân số là 90 người/km ² = Số dân của tỉnh với mật độ 90 người/km ² - Số dân của tỉnh với mật độ 80 người/km ² .

Lời giải chi tiết:

Số dân của tỉnh với mật độ 80 người/km ² là:

10 000 x 80 = 800 000 (người)

Số dân của tỉnh với mật độ 90 người/km ² là:

10 000 x 90 = 900 000 (người)

Muốn tăng mật độ dân số của tỉnh đó là 90 người/km ² thì số dân của tỉnh phải tăng thêm số người là:

900 000 – 800 000 = 100 000 (người)

Đáp số: 100 000 người.