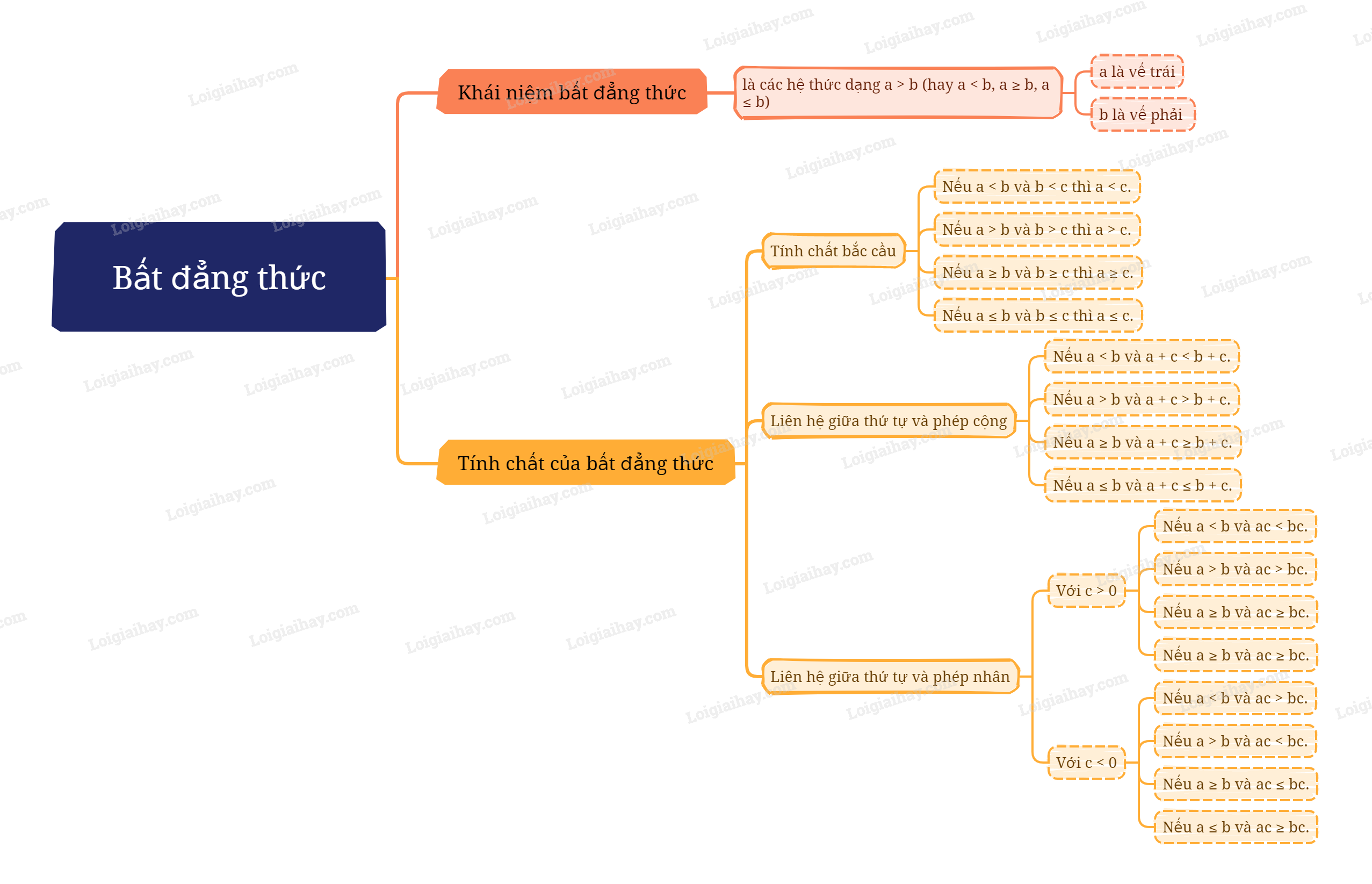
Lý thuyết Bất đẳng thức Toán 9 Chân trời sáng tạo
1. Bất đẳng thức Nhắc lại thứ tự trên tập số thực
1. Bất đẳng thức
Nhắc lại thứ tự trên tập số thực
Trên tập số thực, khi so sánh hai số a và b, xảy ra một trong ba trường hợp sau:
- Số a lớn hơn số b, kí hiệu \(a > b\).
- Số a nhỏ hơn số b, kí hiệu \(a < b\).
- Số a bằng số b, kí hiệu \(a = b\).
Khi biểu diễn số thực trên trục số, điểm biểu diễn số bé hơn nằm trước điểm biểu diễn số lớn hơn.
Nếu \(a > b\) hoặc \(a = b\), ta viết \(a \ge b\) (ta nói a lớn hơn hoặc bằng b hay a không nhỏ hơn b).
Nếu \(a < b\) hoặc \(a = b\), ta viết \(a \le b\) (ta nói a nhỏ hơn hoặc bằng b hay a không lớn hơn b).
Khái niệm bất đẳng thức
|
Hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) là bất đẳng thức và a được gọi là vế trái, b được gọi là vế phải của bất đẳng thức. |
2. Tính chất của bất đẳng thức
Tính chất bắc cầu
|
Cho ba số a, b, c. Nếu \(a < b\) và \(b < c\) thì \(a < c\). Nếu \(a > b\) và \(b > c\) thì \(a > c\). Nếu \(a \le b\) và \(b \le c\) thì \(a \le c\). Nếu \(a \ge b\) và \(b \ge c\) thì \(a \ge c\). |
Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\).
Tính chất liên hệ giữa thứ tự và phép cộng
Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
|
Cho ba số a, b, c. Nếu \(a < b\) thì \(a + c < b + c\). Nếu \(a > b\) thì \(a + c > b + c\). Nếu \(a \le b\) thì \(a + c \le b + c\). Nếu \(a \ge b\) thì \(a + c \ge b + c\). |
Ví dụ: Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\)
Tính chất liên hệ giữa thứ tự và phép nhân
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
|
Với ba số a, b, c và c > 0, ta có: Nếu \(a < b\) thì \(ac < bc\). Nếu \(a > b\) thì \(ac > bc\). Nếu \(a \le b\) thì \(ac \le bc\). Nếu \(a \ge b\) thì \(ac \ge bc\). |
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
|
Với ba số a, b, c và c < 0, ta có: Nếu \(a < b\) thì \(ac > bc\). Nếu \(a > b\) thì \(ac < bc\). Nếu \(a \le b\) thì \(ac \ge bc\). Nếu \(a \ge b\) thì \(ac \le bc\). |
Ví dụ:
Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\).
Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\).