Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
Có các trườn hợp đồng dạng nào của hai tam giác vuông?
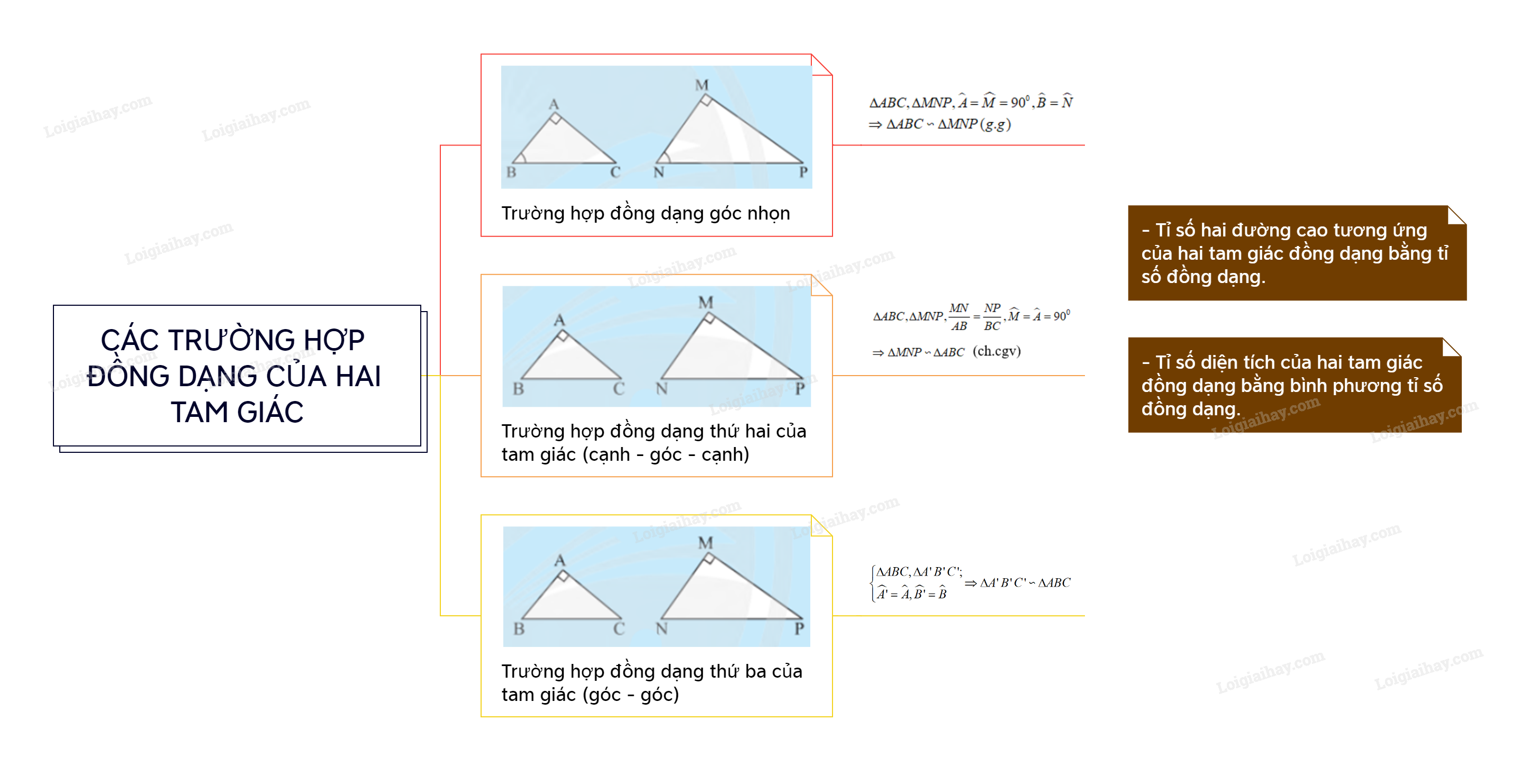
1. Trường hợp góc nhọn
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
\(\begin{array}{l}\Delta ABC,\Delta MNP,\widehat A = \widehat M = {90^0},\widehat B = \widehat N\\ \Rightarrow \Delta ABC \backsim \Delta MNP\,(g.g)\end{array}\)
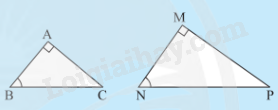
2. Trường hợp hai cạnh góc vuông
Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
\(\Delta ABC,\Delta MNP,\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}},\widehat M = \widehat A = {90^0}\)
\( \Rightarrow \Delta MNP \backsim \Delta ABC\,\)(2cgv)
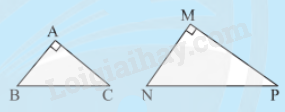
3. Trường hợp cạnh huyền cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng
\(\Delta ABC,\Delta MNP,\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}},\widehat M = \widehat A = {90^0}\)
\( \Rightarrow \Delta MNP \backsim \Delta ABC\,\) (ch.cgv)
Chú ý:
- Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.