Lý thuyết Đa giác đều và phép quay Toán 9 Chân trời sáng tạo
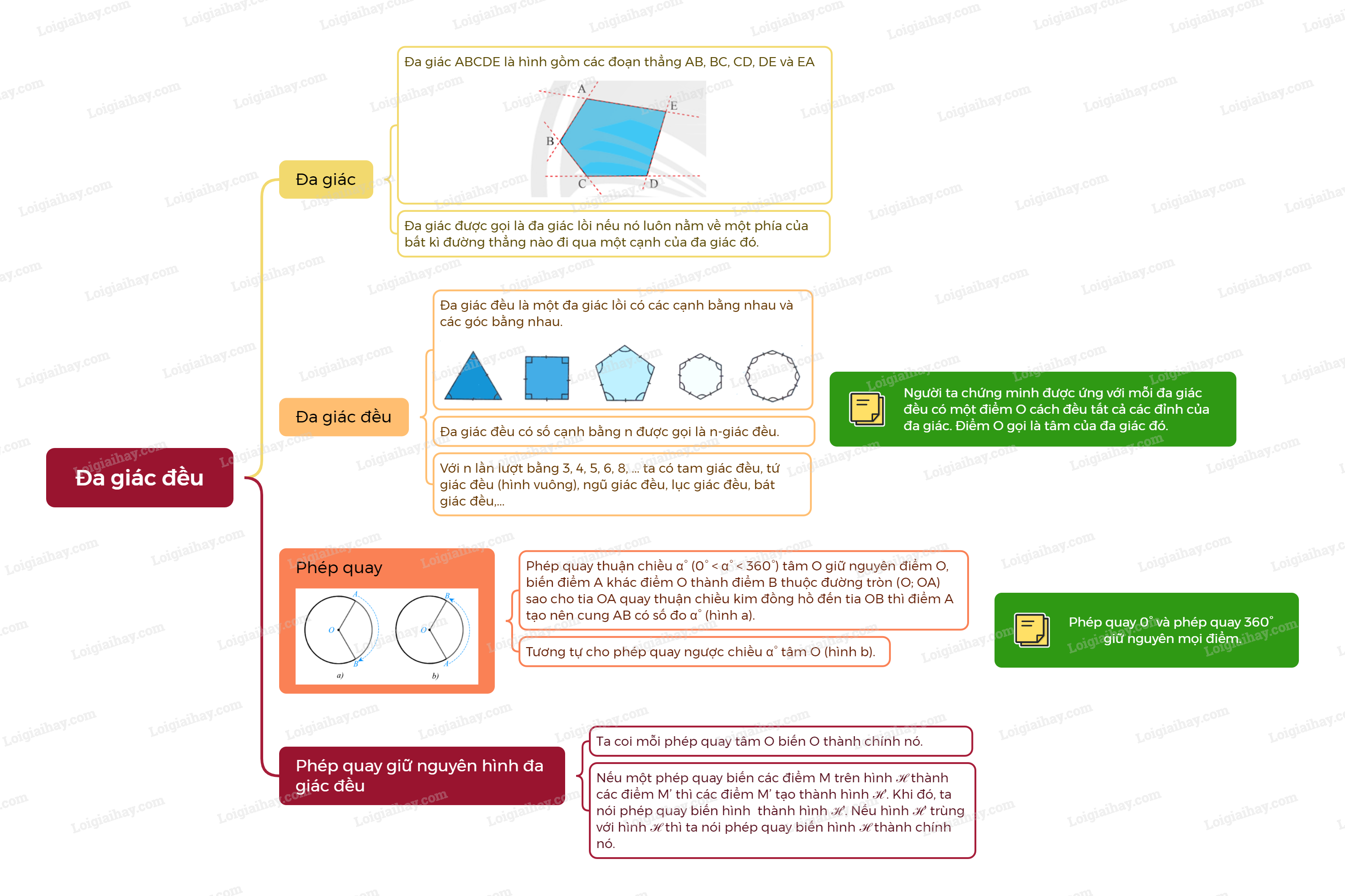
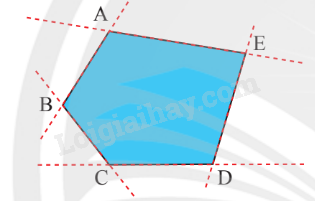
1. Khái niệm đa giác đều Đa giác - Đa giác ABCDE là hình gồm các đoạn thẳng AB, BC, CD, DE và EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
1. Khái niệm đ a giác đều
Đa giác
- Đa giác ABCDE là hình gồm các đoạn thẳng AB, BC, CD, DE và EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
+ Các điểm A, B, C, D, E gọi là các đỉnh .
+ Các đoạn thẳng AB, BC, CD, DE, EA gọi là các cạnh .
+ Các góc \(\widehat {ABC},\widehat {BCD},\widehat {CDE},\widehat {DEA},\widehat {EAB}\) gọi là các góc của đa giác.
- Đa giác được gọi là đa giác lồi nếu nó luôn nằm về một phía của bất kì đường thẳng nào đi qua một cạnh của đa giác đó.
Đa giác đều
|
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau. |
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:

- Đa giác đều có số cạnh bằng n được gọi là n-giác đều.
- Với n lần lượt bằng 3, 4, 5, 6, 8, ... ta có tam giác đều, tứ giác đều (hình vuông), ngũ giác đều, lục giác đều, bát giác đều,...
- Từ nay, khi nói đến đa giác mà không chú thích gì thêm, ta hiểu đó là đa giác lồi.
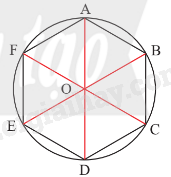
Chú ý: Người ta chứng minh được ứng với mỗi đa giác đều có một điểm O cách đều tất cả các đỉnh của đa giác. Điểm O gọi là tâm của đa giác đó.
2. Phép quay
Khái niệm phép quay
|
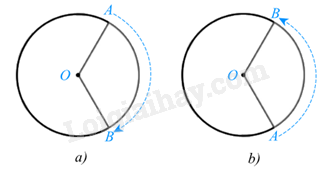
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
|
Phép quay giữ nguyên hình đa giác đều
|
- Ta coi mỗi phép quay tâm O biến O thành chính nó. - Nếu một phép quay biến các điểm M trên hình ℋ thành các điểm M’ thì các điểm M’ tạo thành hình ℋ ’ . Khi đó, ta nói phép quay biến hình thành hình ℋ ’. Nếu hình ℋ ’ trùng với hình ℋ thì ta nói phép quay biến hình ℋ thành chính nó. |
Ví dụ:
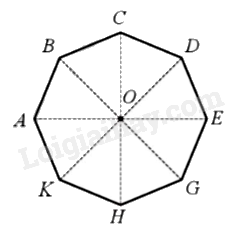
Phép quay thuận chiều \(45^\circ \) tâm O biến điểm A thành điểm B thì phép quay đó biến các điểm C, D, H, K tương ứng thành các điểm D, E, K, A.
3. Hình phẳng đều trong thực tế
Ví dụ: Một số hình phẳng đều trong thực tế: