Lý thuyết Đạo hàm - Toán 11 Chân trời sáng tạo — Không quảng cáo

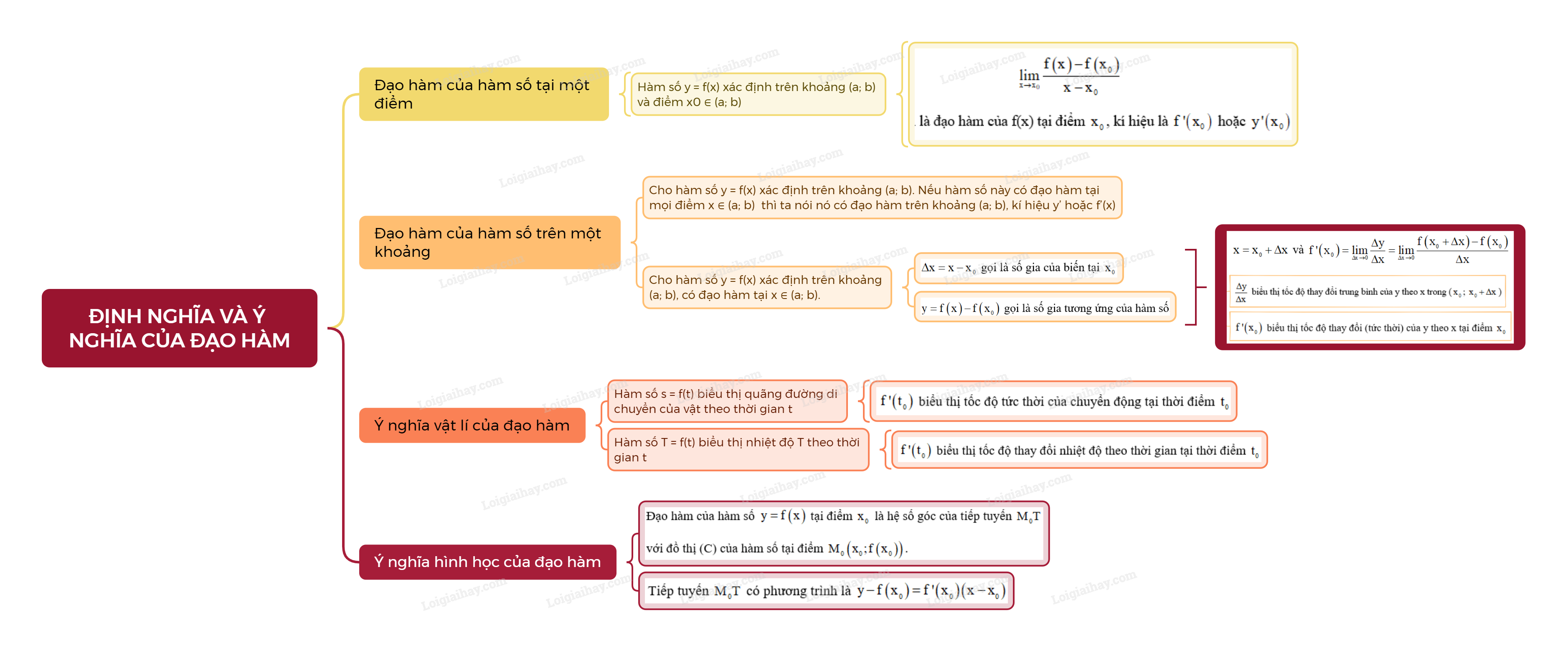
1. Đạo hàm

Cho hàm số y = f(x) xác định trên khoảng $\left( {a;b} \right)$ và điểm ${x_0} \in \left( {a;b} \right)$.

Nếu tồn tại giới hạn (hữu hạn)

$\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$

thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm ${x_0}$, kí hiệu là $f'\left( {{x_0}} \right)$ hoặc $y'\left( {{x_0}} \right)$.

Vậy:

$f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$.

Chú ý:

- Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu hàm số này có đạo hàm tại mọi điểm $x \in \left( {a;b} \right)$ thì ta nói nó có đạo hàm trên khoảng (a; b), kí hiệu y’ hoặc f’(x).

- Cho hàm số y = f(x) xác định trên khoảng (a; b), có đạo hàm tại ${x_0} \in \left( {a;b} \right)$.

a) Đại lượng $\Delta x = x - {x_0}$ gọi là số gia của biến tại ${x_0}$. Đại lượng $y = f\left( x \right) - f\left( {{x_0}} \right)$ gọi là số gia tương ứng của hàm số. Khi đó, $x = {x_0} + \Delta x$ và

$f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)}}{{\Delta x}}$.

b) Tỉ số $\frac{{\Delta y}}{{\Delta x}}$ biểu thị tốc độ thay đổi trung bình của đại lượng y theo đại lượng x trong khoảng từ ${x_0}$ đến ${x_0} + \Delta x$; còn $f'\left( {{x_0}} \right)$ biểu thị tốc độ thay đổi (tức thời) của đại lượng y theo đại lượng x tại điểm ${x_0}$.

2. Ý nghĩa vật lí của đạo hàm

- Nếu hàm số s = f(t) biểu thị quãng đường di chuyển của vật theo thời gian t thì $f'\left( {{t_0}} \right)$ biểu thị tốc độ tức thời của chuyển động tại thời điểm ${t_0}$.

- Nếu hàm số T = f(t) biểu thị nhiệt độ T theo thời gian t thì $f'\left( {{t_0}} \right)$ biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm ${t_0}$.

3. Ý nghĩa hình học của đạo hàm

Đạo hàm của hàm số $y = f\left( x \right)$ tại điểm ${x_0}$ là hệ số góc của tiếp tuyến ${M_0}T$ với đồ thị (C) của hàm số tại điểm ${M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)$.

Tiếp tuyến ${M_0}T$ có phương trình là $y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)$.