Lý thuyết diện tích hình tròn, hình quạt tròn

1. Các kiến thức cần nhớ

Công thức tính diện tích hình tròn

Diện tích $S$ của một hình tròn bán kính $R$ được tính theo công thức $S = \pi {R^2}$

Công thức tính diện tích hình quạt tròn

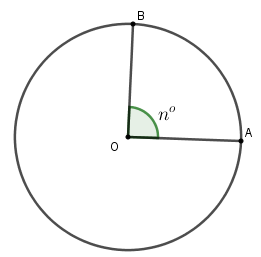
Diện tích hình quạt tròn bán kính $R$ , cung $n^\circ $ được tính theo công thức

$S = \dfrac{{\pi {R^2}n}}{{360}}\,\,hay\,\,\,S = \dfrac{{l.{\rm{R}}}}{2}$ ( với $l$ là độ dài cung $n^\circ $ của hình quạt tròn).

2. Các dạng toán thường gặp

Dạng 1: Tính diện tích hình tròn, diện tích hình quạt tròn và các đại lượng liên quan

Phương pháp:

Áp dụng các công thức tính diện tích hình tròn $S = \pi {R^2}$ và diện tích hình quạt tròn bán kính $R,$ cung $n^\circ $

$S = \dfrac{{\pi {R^2}n}}{{360}}\,\,hay\,\,\,S = \dfrac{{l.{\rm{R}}}}{2}$ (với $l$ là độ dài cung $n^\circ $của hình quạt tròn)

Dạng 2 : Bài toán tổng hợp

Phương pháp :

Sử dụng linh hoạt các kiến thức đã học để tính góc ở tâm, bán kinh đường tròn. Từ đó tính được diện tích hình tròn và diện tích hình quạt tròn.

Cùng chủ đề:

Lý thuyết diện tích hình tròn, hình quạt tròn