Lý thuyết Đơn thức nhiều biến SGK Toán 8 - Cùng khám phá
Đơn thức nhiều biến là gì?
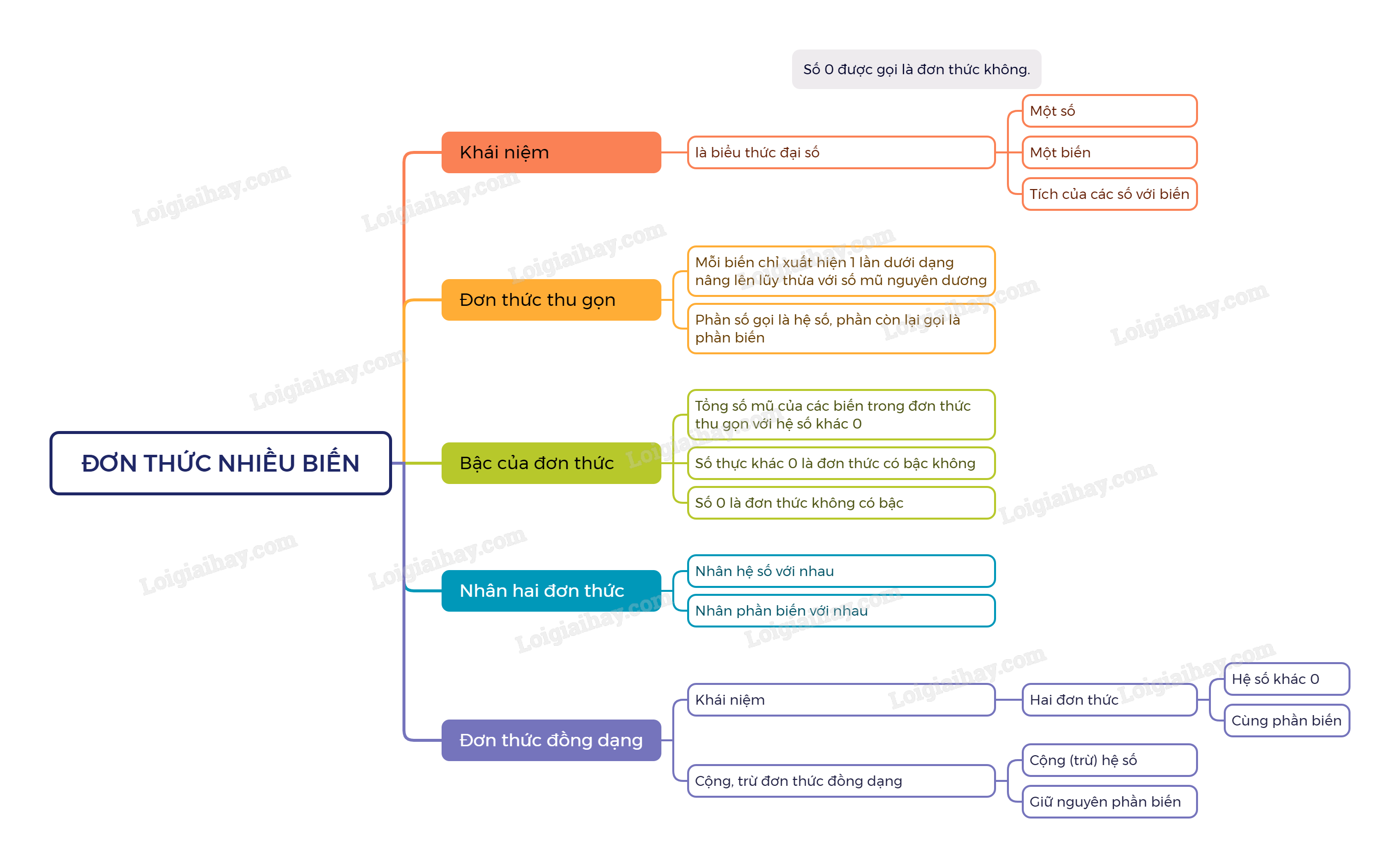
1. Khái niệm
Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và các biến.
Số 0 được gọi là đơn thức không.
Ví dụ: \(1;2xy; - \frac{3}{4}{x^2}y( - 4x);...\) là các đơn thức.
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến, mà mỗi biến chỉ có mặt một lần dưới dạng một lũy thừa với số mũ nguyên dương.
Ví dụ:
\(1;2xy;5{x^2}{y^4}z;...\) là các đơn thức thu gọn.
\(3{x^2}yx; - \frac{3}{4}{x^2}y( - 4x);...\) không phải là các đơn thức thu gọn.
Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó. Bậc của một đơn thức có hệ số khác 0 bằng với bậc của đơn thức thu gọn của nó.
Chú ý: + Số thực khác 0 là đơn thức bậc không.
+ Số 0 được gọi là đơn thức không có bậc.
Ví dụ: \(2xy\) có bậc là \(1 + 1 = 2\)
\(5{x^2}{y^4}z\) có bậc là \(2 + 4 + 1 = 7\)
Trong một đơn thức thu gọn, phần số còn gọi là hệ số , phần còn lại gọi là phần biến.
Ví dụ: đơn thức \(3{x^3}.y\) có hệ số là 3, phần biến là \({x^3}.y\).
2. Nhân hai đơn thức
Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau.
Ví dụ: \(( - 3{x^2}y)(4xy) = \left[ {\left( { - 3.4} \right)} \right].({x^2}.x).\left( {y.y} \right) = - 12.{x^3}.{y^2}\)
3. Đơn thức đồng dạng
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Ví dụ:
Hai đơn thức \(5{x^2}{y^4}z\) và \( - \frac{1}{3}{x^2}{y^4}z\) có hệ số khác 0 và có cùng phần biến nên chúng là hai đơn thức đồng dạng.
Hai đơn thức \(5{x^2}{y^4}z\) và \(5x{y^2}z\) không có cùng phần biến nên chúng không phải là hai đơn thức đồng dạng.
Cộng, trừ các đơn thức đồng dạng
Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
Ví dụ:
\(\begin{array}{l}2{x^3}{y^2} + 4{x^3}{y^2} = 6{x^3}{y^2}\\4a{y^2} - 3a{y^2} = a{y^2}\end{array}\)