Lý thuyết Xác suất của biến cố ngẫu nhiên SGK Toán 8 - Cùng khám phá
Xác suất của biến cố ngẫu nhiên là gì?
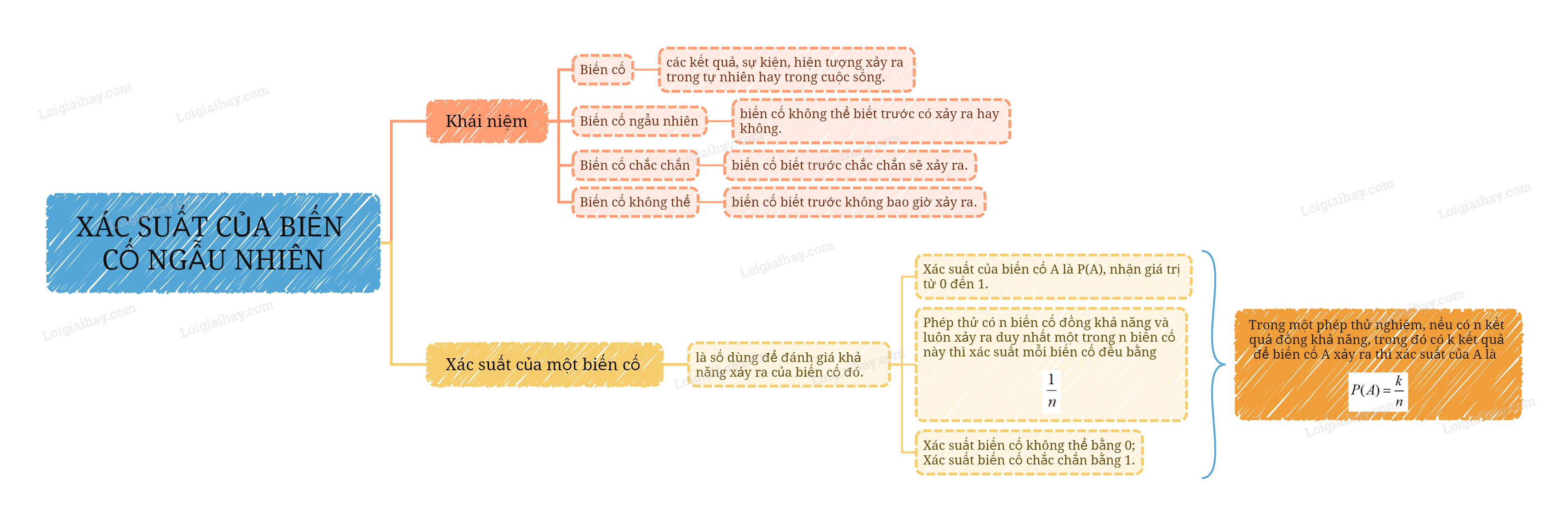
1. Biến cố, biến cố ngẫu nhiên
- Biến cố là các kết quả, sự kiện, hiện tượng xảy ra trong tự nhiên hay trong cuộc sống.
- Biến cố ngẫu nhiên là biến cố không thể biết trước có xảy ra hay không.
- Biến cố biết trước chắc chắn sẽ xảy ra được gọi là biến cố chắc chắn .
- Biến cố biết trước không bao giờ xảy ra được gọi là biến cố không thể .
2. Xác suất của một biến cố
Xác suất của một biến cố là số được dùng để đánh giá khả năng xảy ra của biến cố đó.
- Xác suất của biến cố A, kí hiệu là P(A), là một số nhận giá trị từ 0 đến 1.
- Nếu phép thử nghiệm có n biến cố đồng khả năng và luôn xảy ra duy nhất một trong n biến cố này thì xác suất của mỗi biến cố đều bằng \(\frac{1}{n}\).
- Xác suất của biến cố không thể bằng 0. Xác suất của biến cố chắc chắn bằng 1.
Tổng quát:
Trong một phép thử nghiệm, nếu có n kết quả đồng khả năng, trong đó có k kết quả để biến cố A xảy ra thì xác suất của A là \(P(A) = \frac{k}{n}\).
Để tiện cho tính toán, so sánh, người ta thường viết xác suất của biến cố dưới dạng số thập phân hoặc dạng phần trăm.