Lý thuyết Đường thẳng và mặt phẳng song song - SGK Toán 11 Cánh Diều — Không quảng cáo

I. Đường thẳng song song với mặt phẳng

Đường thẳng được gọi là song song với mặt phẳng nếu chúng không có điểm chung.

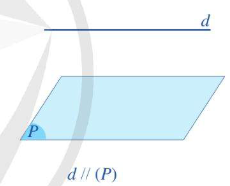
*Nhận xét:

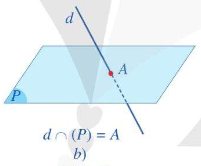
- Nếu d và \(\left( P \right)\) có một điểm chung duy nhất thì ta nói d và \(\left( P \right)\) cắt nhau tại A. Kí hiệu \(d \cap \left( P \right) = A\)hay \(d \cap \left( P \right) = \left\{ A \right\}\).

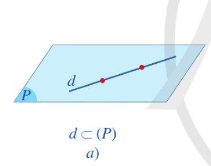
- Nếu d và \(\left( P \right)\) có nhiều hơn 1 điểm chung thì ta nói d nằm trong \(\left( P \right)\) hay \(\left( P \right)\) chứa d. Kí hiệu \(d \subset \left( P \right)\)hay \(\left( P \right) \supset d\).

II. Điều kiện và tính chất

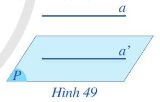
• Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với một đường thẳng a’ nằm trong (P) thì ta nói \(a//\left( P \right)\).

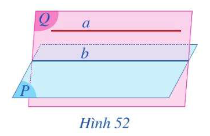
• Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b//a.

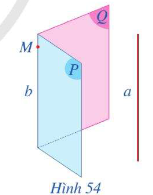
• Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.