Lý thuyết Đường tròn. Vị trí tương đối của hai đường tròn Toán 9 Cánh diều
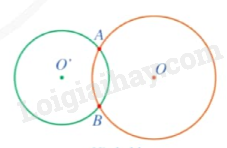
1. Khái niệm đường tròn Trong mặt phẳng, đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng bằng R (R > 0), kí hiệu là (O;R).
1. Khái niệm đường tròn
|
Trong mặt phẳng, đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng bằng R (R > 0), kí hiệu là (O;R). |
Chú ý:
- Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
- Khi không quan tâm đến bán kính của đường tròn (O;R), ta cũng có thể kí hiệu đường tròn là (O).
Vị trí tương đối của điểm và đường tròn
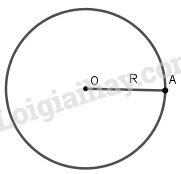
Cho đường tròn (O; R) và điểm M. Khi đó:
- Nếu điểm M thuộc đường tròn (O) (hay ta còn nói điểm M nằm trên đường tròn (O), hoặc đường tròn (O) đi qua điểm M) thì OM = R và ngược lại.
- Nếu điểm M nằm bên trong (hay nằm trong, ở trong) đường tròn (O) thì OM < R và ngược lại.
- Nếu điểm M nằm bên ngoài (hay nằm ngoài, ở ngoài) đường tròn (O) thì OM > R và ngược lại.
2. Liên hệ giữa đường kính và dây của đường tròn
Chú ý:
- Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung ) của đường tròn.
- Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường kính.
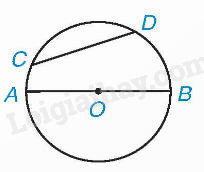
Ví dụ: Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
3 . Tính đối xứng của đường tròn
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua tâm của đường tròn cũng nằm trên đường tròn đó.
|
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. |
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua một đường thẳng đi qua tâm của đường tròn cũng nằm trên đường tròn đó.
|
Đường tròn là hình có trục đối xứng. Mỗi đường thẳng đi qua tâm là một trục đối xứng của đường tròn đó. |
Ví dụ:
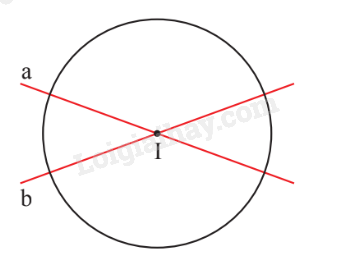
Hình tròn tâm I có:
I là tâm đối xứng;
Đường thẳng a, b là các trục đối xứng của hình tròn (I).
4. Vị trí tương đối của hai đường tròn
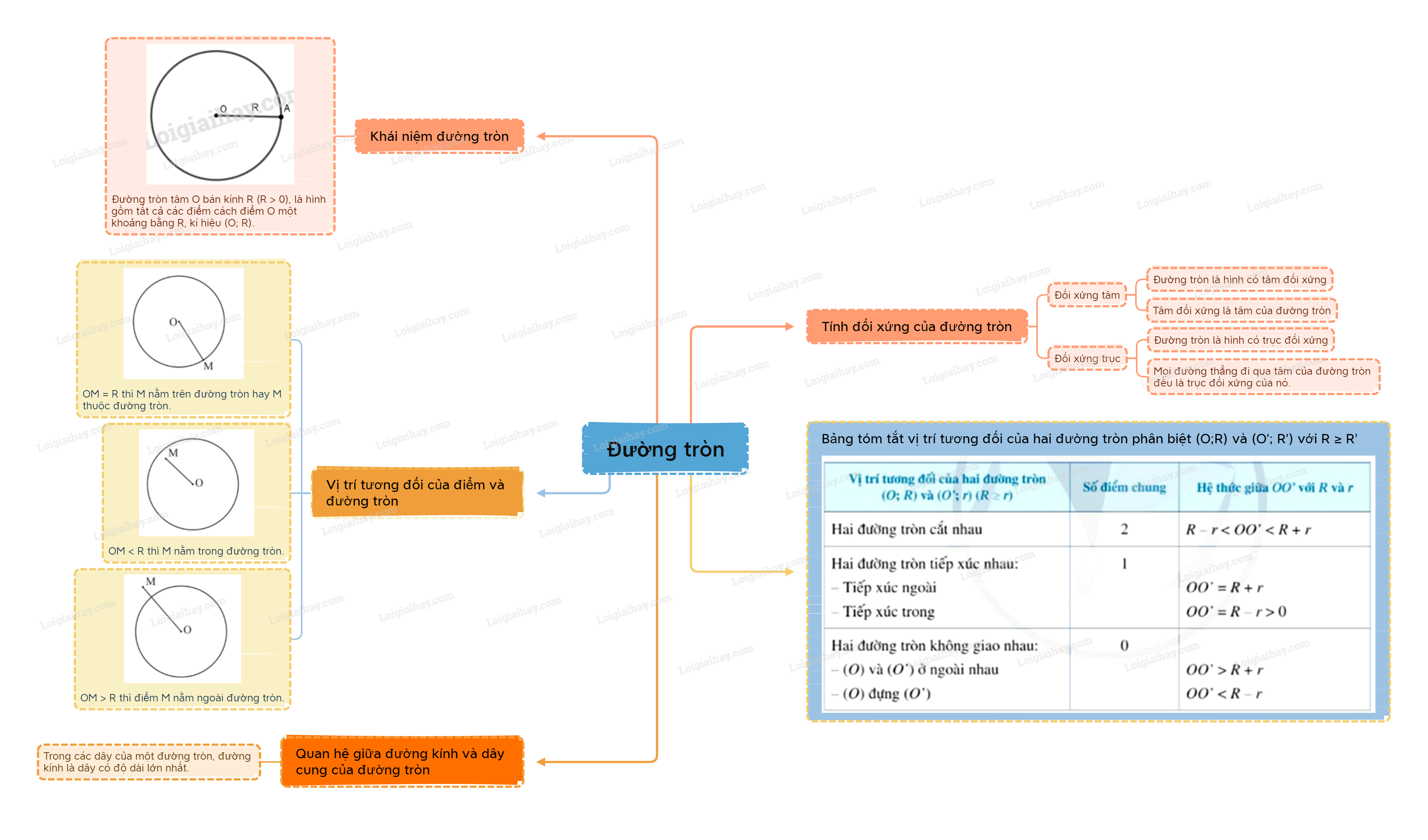
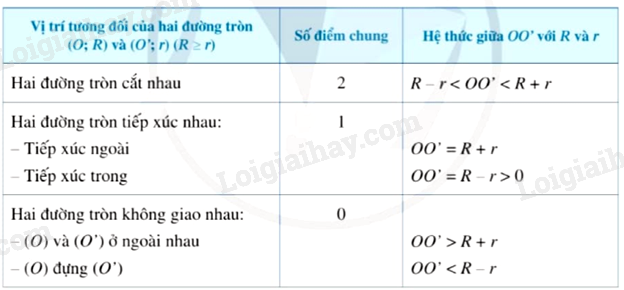
Hai đường tròn cắt nhau
|
Hai đường tròn có đúng hai điểm chung gọi là hai đường tròn cắt nhau.
|
Mỗi điểm chung của hai đường tròn cắt nhau được gọi là một giao điểm của hai đường tròn đó.
Nếu hai đường tròn (O;R) và (O’;r) với \(R \ge r\) cắt nhau thì \(R - r < OO' < R + r\).
Hai đường tròn tiếp xúc nhau
|
Hai đường tròn có đúng một điểm chung gọi là hai đường tròn tiếp xúc nhau (tại điểm chung đó). |
Điểm chung của hai đường tròn tiếp xúc nhau được gọi là tiếp điểm.
Có hai trường hợp về hai đường tròn tiếp xúc nhau:
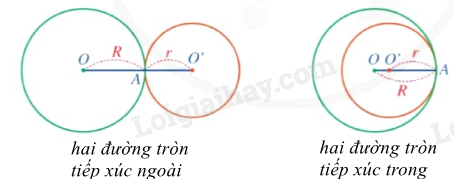
Nếu hai đường tròn (O;R) và (O’;r) tiếp xúc ngoài thì tiếp điểm A nằm giữa O, O’ và \(OO' = R + r\). Điều ngược lại cũng đúng.
Với R > r, nếu hai đường tròn (O;R) và (O’;r) tiếp xúc trong thì điểm O’ nằm giữa O, A và \(OO' = R - r\). Điều ngược lại cũng đúng.
Hai đường tròn không giao nhau
|
Hai đường tròn không có điểm chung gọi là hai đường tròn không giao nhau . |
Có hai trường hợp về hai đường tròn không giao nhau:

Nếu hai đường tròn (O;R) và (O’;r) ở ngoài nhau thì \(OO' > R + r\). Điều ngược lại cũng đúng.
Với R > r, nếu đường tròn (O) đựng đường tròn (O’) thì \(OO' > R - r\). Điều ngược lại cũng đúng.
Nhận xét: Ta có thể nhận biết vị trí tương đối của hai đường tròn \(\left( {O;R} \right),\left( {O';r} \right)\left( {R \ge r} \right)\) thông qua hệ thức liên hệ giữa OO’ với R và r được tóm tắt trong bảng sau:
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có \(OO' > 8cm\) thì \(OO' = 8cm > 3cm + 4cm = R + R'\) nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.