Lý thuyết Đa giác đều. Hình đa giác đều trong thực tiễn Toán 9 Cánh diều
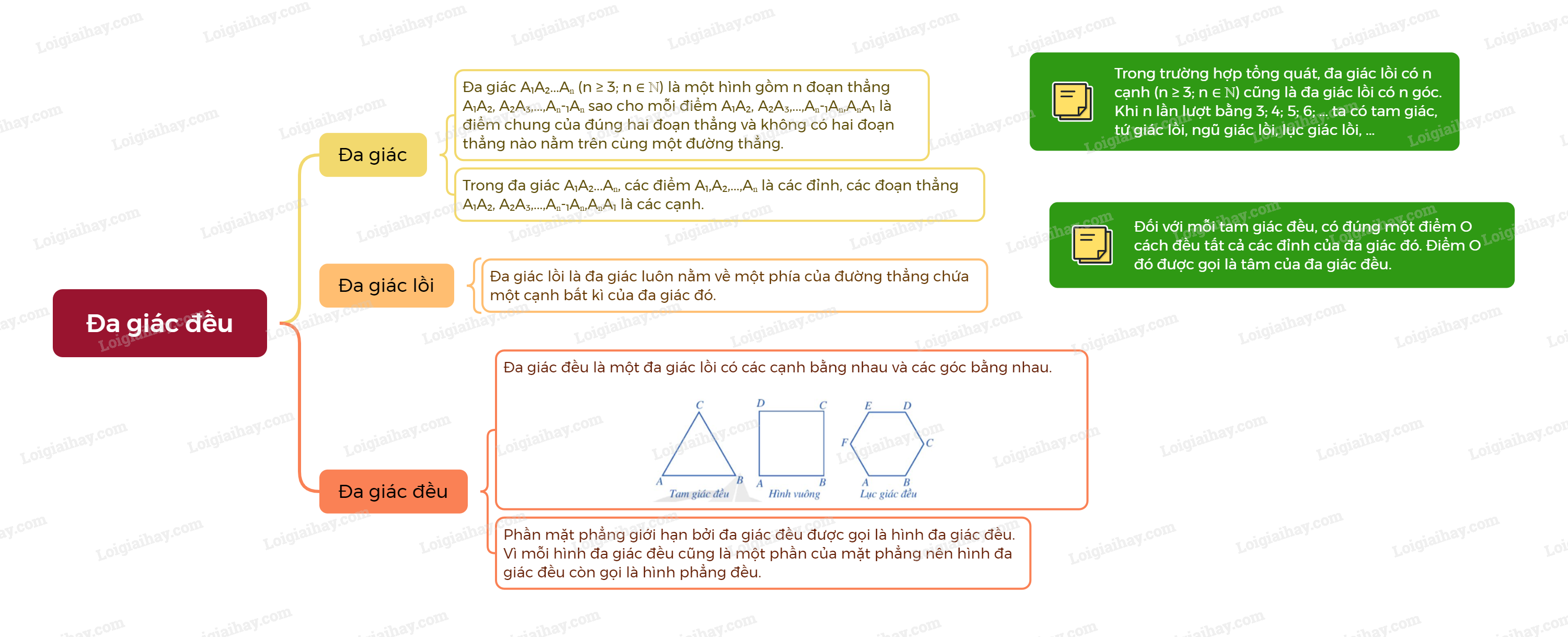
1. Đa giác, đa giác lồi Đa giác Đa giác \({A_1}{A_2}...{A_n}\left( {n \ge 3;n \in \mathbb{N}} \right)\) là một hình gồm n đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) sao cho mỗi điểm \({A_1},{A_2},...,{A_n}\) là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác \({A_1}{A_2}...{A_n}\), các điểm \({A_1},{A_2},...,{A_n}\) là các đỉnh, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) là c
1. Đa giác, đa giác lồi
Đa giác
|
Đa giác \({A_1}{A_2}...{A_n}\left( {n \ge 3;n \in \mathbb{N}} \right)\) là một hình gồm n đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) sao cho mỗi điểm \({A_1},{A_2},...,{A_n}\) là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác \({A_1}{A_2}...{A_n}\), các điểm \({A_1},{A_2},...,{A_n}\) là các đỉnh, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) là các cạnh. |
Đa giác lồi
|
Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó. |
Ví dụ:
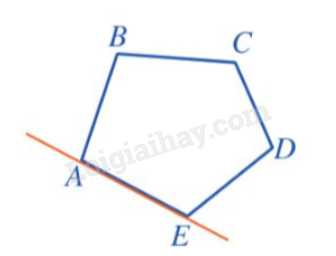
- Do ngũ giác ABCDE luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của ngũ giác đó nên ta nói ngũ giác ABCDE là ngũ giác lồi.
- Với ngũ giác lồi ABCDE, các góc ABC, BCD, CDE, DEA, EAB gọi là các góc của đa giác.
Trong trường hợp tổng quát, đa giác lồi có n cạnh (\(n \ge 3\), \(n \in N\)) cũng là đa giác lồi có n góc. Khi n lần lượt bằng 3; 4; 5; 6; ... ta có tam giác, tứ giác lồi, ngũ giác lồi, lục giác lồi, ...
Quy ước: Từ nay về sau, khi nói về đa giác mà không chú thích gì thêm thì ta hiểu đó là đa giác lồi.
2. Đa giác đều
|
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau. |
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:
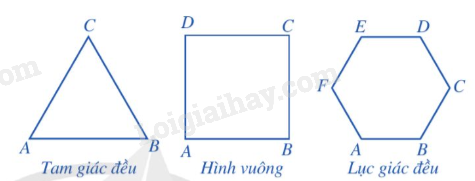
Nhận xét: Đối với mỗi tam giác đều, có đúng một điểm O cách đều tất cả các đỉnh của đa giác đó. Điểm O đó được gọi là tâm của đa giác đều.
Chú ý: Phần mặt phẳng giới hạn bởi đa giác đều được gọi là hình đa giác đều. Vì mỗi hình đa giác đều cũng là một phần của mặt phẳng nên hình đa giác đều còn gọi là hình phẳng đều.
3. Hình đa giác đều trong thực tiễn
Trong thế giới tự nhiên, trong nghệ thuật kiến trúc và thiết kế công nghệ, vật thể có hình ảnh liên quan đến hình đa giác đều rất đa dạng và phong phú.