Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

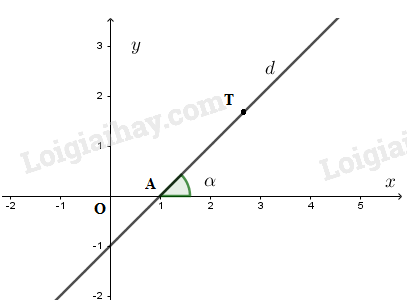
Gọi A là giao điểm của đường thẳng

1. Góc tạo bởi đường thẳng $y = ax + b (a ≠ 0)$ và trục $Ox.$

Gọi $A$ là giao điểm của đường thẳng $d:y = ax + b$ với trục $Ox$ và $T$ là một điểm thuộc đường thẳng, nằm phía trên trục $Ox.$ Khi đó góc $\alpha=\widehat {TAx}$ được gọi là góc tạo bởi đường thẳng $d: y = ax + b$ và trục $Ox.$

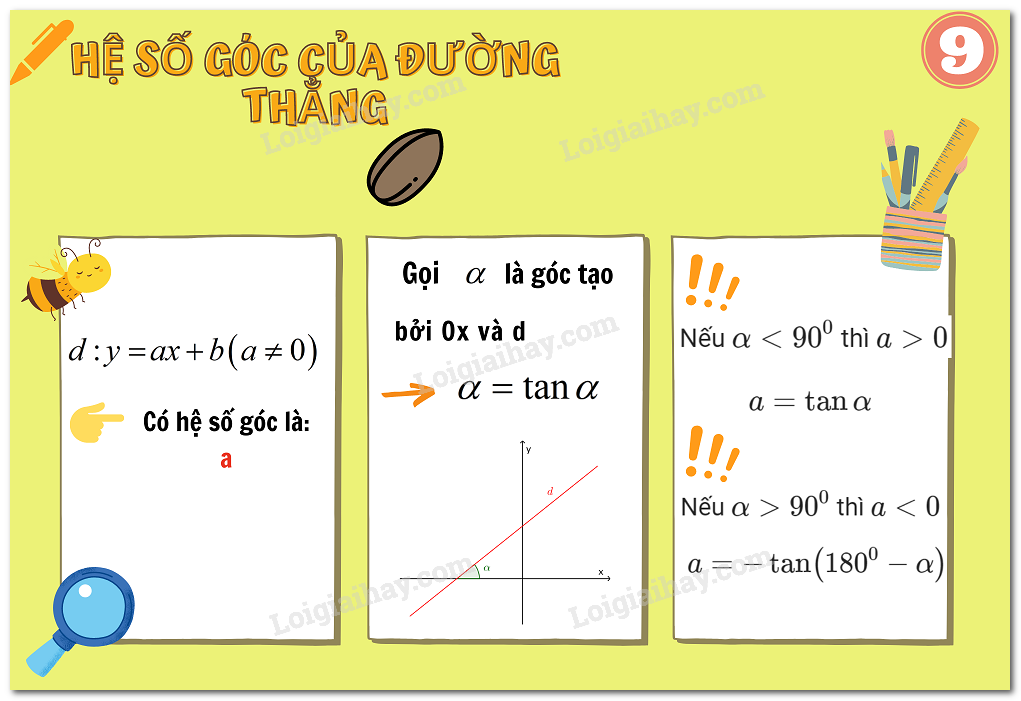
2. Hệ số góc của đường thẳng $y = ax + b (a ≠ 0)$

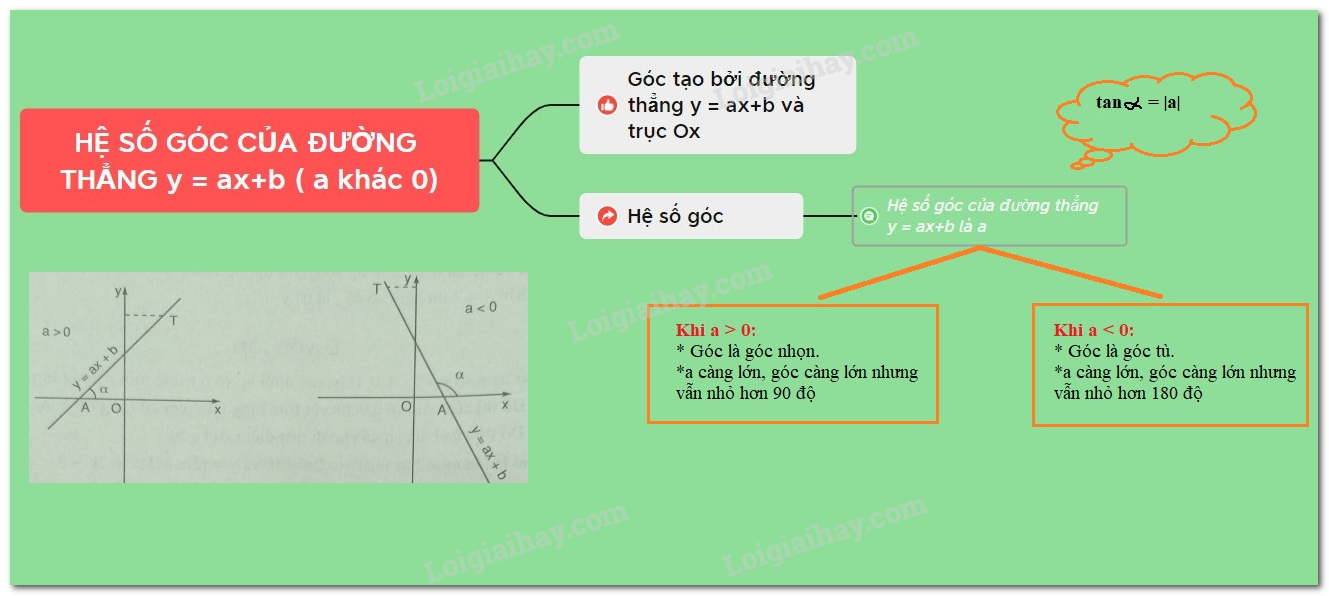
+) Khi $a > 0,$ góc tạo bởi đường thẳng $y = ax + b$ và trục $Ox$ là góc nhọn và nếu $a$ càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn $90^0.$

+) Khi $a < 0,$ góc tạo bởi đường thẳng $y = ax + b$ và trục $Ox$ là góc tù và nếu $|a|$ càng bé thì góc đó càng lớn nhưng vẫn nhỏ hơn $180^0.$

Như vậy, góc tạo bởi đường thẳng $d: y = ax + b$ và trục $Ox$ phụ thuộc vào $a.$

Người ta gọi $a$ là hệ số góc của đường thẳng $y = ax + b.$

Lưu ý:

+) Khi $a > 0,$ ta có $\tan \alpha= a.$

+) Khi $a < 0,$ ta có $\tan (180^0-\alpha) = -a.$

Từ đó tìm được số đo của góc $180^0-\alpha$ rồi suy ra số đo của góc $\alpha.$

+) Các đường thẳng có cùng hệ số $a$ ($a$ là hệ số của $x$) thì tạo với trục $Ox$ các góc bằng nhau.

3. Các dạng toán cơ bản

Dạng 1: Xác định hệ số góc của đường thẳng

Phương pháp:

Đường thẳng $(d)$ có phương trình $y = ax + b\,\left( {a \ne 0} \right)$ có $a$ là hệ số góc.

Ví dụ: Hệ số góc của đường thẳng $y=-2x+1$ là $a=-2$

Dạng 2: Tính góc tạo bởi tia $Ox$ và đường thẳng $(d).$

Phương pháp:

Gọi $\alpha $ là góc tạo bởi tia $Ox$ và $d.$ Ta có: $a = \tan \alpha $

Ví dụ: Góc tạo bởi tia $Ox$ và đường thẳng $(d):y=\sqrt 3 x+1$ là $\alpha $

Khi đó: $\tan \alpha=\sqrt 3$ nên $\alpha =60^0$

Dạng 3. Viết phương trình đường thẳng hoặc tìm tham số m khi biết hệ số góc

Phương pháp:

Gọi phương trình đường thẳng cần tìm là $y = ax + b\,\,\left( {a \ne 0} \right)$.

Dựa vào lý thuyết về hệ số góc để tìm $a$. Từ đó, sử dụng dữ kiện còn lại của đề bài để tìm $b$.

4. Bài tập về hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Bài 1. Cho đường thẳng $d$:$y = ax + b\,\,\left( {a \ne 0} \right)$. Hệ số góc của đường thẳng $d$ là

A. $ - a$

B. $a$

C. $\dfrac{1}{a}$

D. $b$

Lời giải:

Đường thẳng $d$ có phương trình $y = ax + b\,\left( {a \ne 0} \right)$có $a$ là hệ số góc.

Chọn đáp án B.

Bài 2. Cho đường thẳng $d$:$y = ax + b\,\,\left( {a > 0} \right)$. Gọi $\alpha $ là góc tạo bởi tia $Ox$ và $d.$ Khẳng định nào dưới đây là đúng ?

A. $a = - \tan \alpha $

B. $a = \tan \left( {180 - \alpha } \right)$

C. $a = \tan \alpha $

D. $a = - \tan \left( {180^\circ - \alpha } \right)$

Lời giải: Cho đường thẳng $d$ có phương trình $y = ax + b\,\left( {a \ne 0} \right)$.

Gọi $\alpha $ là góc tạo bởi tia $Ox$ và $d.$ Ta có: $a = \tan \alpha $

Chọn đáp án C.

Bài 3. Cho đường thẳng $d$:$y = 2x + 1$. Hệ số góc của đường thẳng $d$ là

A. $ - 2$

B. $\dfrac{1}{2}$

C. $1$

D. $2$

Lời giải: Đường thẳng $d$:$y = 2x + 1$ có hệ số góc là $a = 2$.

Chọn đáp án D.

Bài 4. Cho đường thẳng $d:$ $y = \left( {m + 2} \right)x - 5$ đi qua điểm $A\left( { - 1;2} \right)$. Hệ số góc của đường thẳng $d$ là

A. $1$

B. $11$

C. $ -7$

D. $7$

Lời giải: Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ ta được $\left( {m + 2} \right).\left( { - 1} \right) - 5 = 2 \Leftrightarrow -m-2=7\Leftrightarrow m = -9$

Suy ra $d:y = -7x - 5$

Hệ số góc của đường thẳng $d$ là $k = -7$.

Chọn đáp án C.

Bài 5. Tìm hệ số góc của đường thẳng $d$ biết $d$ đi qua gốc tọa độ $O$ và điểm $M\left( {1;3} \right)$

A. $ - 2$

B. $3$

C. $1$

D. $2$

Lời giải:

Gọi phương trình đường thẳng $d$cần tìm là $y = ax + b\,$ $ \left( {a \ne 0} \right)$

Vì $d$ đi qua gốc tọa độ nên $b = 0$$ \Rightarrow y = ax$

Thay tọa độ điểm $M$ vào phương trình $y = ax$ ta được $3 = 1.a \Rightarrow a = 3$ (TM)