Lý thuyết Phép cộng, phép trừ các số tự nhiên Toán 6 Cánh diều — Không quảng cáo

1. Phép cộng

\(a + b = c\)

(số hạng) + (số hạng) = (tổng)

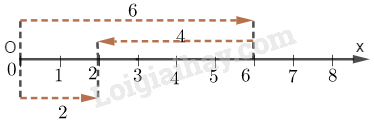
Minh họa trên tia số:

Phép cộng 2+4=6: tổng hai tia bên trên bằng tia bên dưới.

Tính chất của phép cộng:

Giao hoán: \(a + b = b + a\)

Kết hợp: \(\left( {a + b} \right) + c = a + \left( {b + c} \right) = a + b + c\)

\(a + b + c\) được gọi là tổng của ba số \(a,b,c\)

Cộng với số 0: \(a + 0 = 0 + a = a\)

Lưu ý: Khi cộng nhiều số, ta nên nhóm các số hạng có tổng là số chẵn tròn chục , tròn trăm ,...(nếu có).

Ví dụ:

Tính một cách hợp lí: 12+25+15+28

Nhận xét: Ta thấy nếu tính riêng 12+28 và 25+15 thì được: 12+28=40 và 25+15=40 kết quả của hai phép tính này là tròn chục nên ta thực hiện phép tính sau:

12+25+15+28

= 12+28+25+15 (Đổi vị trí của các số 25, 15, 28: Tính chất giao hoán)

= (12+28)+(25+15) (Kết hợp)

= 40+40

= 80

2. Phép trừ

Cho hai số tự nhiên \(a\)  và \(b,\)  nếu có số tự nhiên \(x\)  sao cho \(b + x = a\) thì ta có phép trừ

\(a - b = x\)

(số bị trừ) - (số trừ) = (hiệu)

Chú ý: Điều kiện để thực hiện được phép trừ là số bị trừ lớn hơn hoặc bằng số trừ.

Minh họa trên tia số:

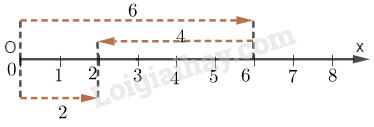
CÁC DẠNG TOÁN VỀ PHÉP CỘNG, PHÉP TRỪ SỐ TỰ NHIÊN

I. Thực hiện phép cộng, trừ

Phương pháp:

- Cộng các số theo “hàng ngang” hoặc theo “hàng dọc”

- Sử dụng máy tính bỏ túi (đối với những bài được phép dùng )

II. Áp dụng các tính chất của phép cộng để tính nhanh

Phương pháp:

- Quan sát, phát hiện các đặc điểm của các số hạng.

- Từ đó, xét xem nên áp dụng tính chất nào (giao hoán, kết hợp) để tính một cách nhanh chóng.

Đặc biệt: Viết một số dưới dạng một tổng để tính một cách hợp lí

Phương pháp:

Bước 1: Căn cứ theo yêu cầu của đề bài, ta có thể viết một số tự nhiên đã cho dưới dạng một tổng của hai hay nhiều số hạng.

Bước 2: Sử dụng tính chất giao hoán, kết hợp để tính một cách hợp lí.

III. Tìm số chưa biết trong một đẳng thức

Với phép cộng: Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: một số hạng bằng tổng của hai số trừ số hạng kia…

Với phép trừ: + Để tìm số bị trừ ta lấy hiệu cộng với số trừ

+ Để tìm số trừ, ta lấy số bị trừ trừ đi số trừ

Ví dụ:

Tìm số tự nhiên $x$ biết: $x+1=5$

Giải:

$x+1=5$

$x$        $=5-1$

$x$        $=4$

IV. So sánh hai tổng mà không tính cụ thể giá trị của chúng

Phương pháp:

Nhận xét, phát hiện và sử dụng các đặc điểm của các số hạng trong tổng. Từ đó dựa vào các tính chất của phép cộng để rút ra kết luận.

Ví dụ:

So sánh hai tổng $1367+5472$ và $5377+1462$ mà không tính giá trị cụ thể của chúng.

Giải:

Đặt \(A=1367+5472\) và \(B=5377+1462\)

\(A=1367+5472\)

\(A=1000+300+67+5000+400+62+10\)

\(A=5000+1000+400+300+67+62+10\)

\(B=5377+1462\)

\(B=5000+300+67+10+1000+400+62\)

\(B=5000+1000+400+300+67+62+10\)

Vậy A = B