Lý thuyết Tập hợp, các phép toán trên tập hợp - SGK Toán 10 Cánh diều
I. TẬP HỢP II. TẬP CON VÀ TẬP HỢP BẰNG NHAU
I. TẬP HỢP
+) Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng (viết là \(\emptyset \))
+) Một tập hợp có thể không có phần tử nào, cũng có thể có một phần tử, có nhiều phần tử, có vô số phần tử
II. TẬP CON VÀ TẬP HỢP BẰNG NHAU
1. Tập con
\(A \subset B \Leftrightarrow (\forall x,x \in A \Rightarrow x \in B)\)
+) Khi \(A \subset B\), ta cũng viết \(B \supset A\)
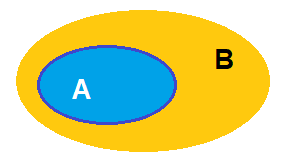
+) Nếu A không phải là tập con của B, ta viết \(A\not{ \subset }B\)
* Nhận xét:
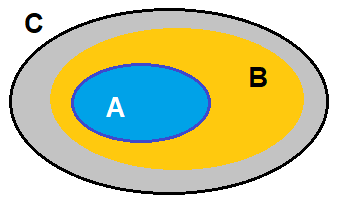
+) \(A \subset A\;\forall A\)
+) \(A \subset B,B \subset C \Rightarrow A \subset C\)
2. Tập hợp bằng nhau
\(A = B \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)
III. GIAO CỦA HAI TẬP HỢP
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
IV. HỢP CỦA HAI TẬP HỢP
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
V. PHẦN BÙ. HIỆU CỦA HAI TẬP HỢP
\(A{\rm{\backslash }}B = \{ x|x \in A\) và \(x \notin B\} \) (Hiệu của A và B)
\(A \subset B\), kí hiệu: \({C_B}A = B{\rm{\backslash }}A\) (Phần bù của A trong B)
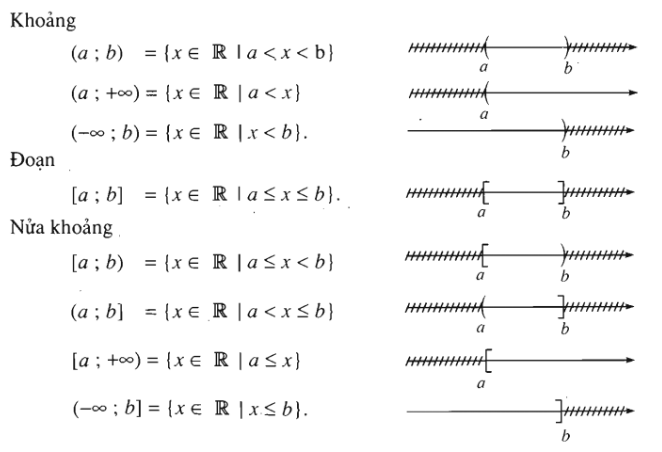
VI. CÁC TẬP HỢP SỐ
\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
Một số tập con thường dùng