Lý thuyết Tính đơn điệu và cực trị của hàm số Toán 12 Kết nối tri thức

1. Tính đơn điệu của hàm số Khái niệm tính đơn điệu của hàm số

1. Tính đơn điệu của hàm số

Khái niệm tính đơn điệu của hàm số

Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là hàm số xác định trên K

Hàm số y = f(x) đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
Hàm số y = f(x) nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)

Ví dụ: Hàm số y = |x| đồng biến trên khoảng \(\left( {0; + \infty } \right)\), nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\)

Định lý

Cho hàm số y = f(x) có đạo hàm trên khoảng K.

Hàm số y = f(x) đồng biến trên khoảng K nếu f’(x) > 0
Hàm số y = f(x) đồng biến trên khoảng K nếu f’(x) < 0

Ví dụ: Hàm số \(y = {x^2} - 4x + 2\) có y’ = 2x – 4

y’ > 0 với \(x \in (2; + \infty )\) nên HS đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
y’ < 0 với \(x \in ( - \infty ;2)\) nên HS đồng biến trên khoảng \(\left( { - \infty ;2} \right)\)

Sử dụng BBT xét tính đơn điệu của hàm số

Các bước để xét tính đơn điệu của hàm số y = f(x)

Tìm tập xác định của hàm số.
Tính đạo hàm f’(x). Tìm các điểm \({x_i}\)(i=1,2,…) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập BBT của hàm số.
Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Ví dụ: Xét chiều biến thiên của hàm số \(y = \frac{{x - 2}}{{x + 1}}\)

1. Tập xác định của hàm số là \(R\backslash \left\{ { - 1} \right\}\)

2. Ta có: \(y' = \frac{{(x + 1) - (x - 2)}}{{{{(x + 1)}^2}}} = \frac{3}{{{{(x + 1)}^2}}} > 0\forall x \ne - 1\)

3. BBT

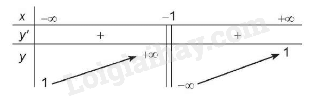
4. Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\)

2. Cực trị của hàm số

Khái niệm cực trị của hàm số

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b) (a có thể là \( - \infty \), b có thể là \( + \infty \) ) và điểm \({x_0} \in \left( {a;b} \right)\).

Nếu tồn tại số h > 0 sao cho f(x) < f(\({x_0}\)) \(\forall x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì hàm số f(x) đạt cực đại tại \({x_0}\)
Nếu tồn tại số h > 0 sao cho f(x) > f(\({x_0}\)) \(\forall x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì hàm số f(x) đạt cực tiểu tại \({x_0}\)

Ví dụ: Cho đồ thị của hàm số y = f(x) như sau

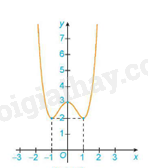
Hàm số đạt cực tiểu tại x = -1 và \({y_{CT}}\)= y(-1) = 2

Hàm số đạt cực đại tại x = 0 và = y(0) = 3

Hàm số đạt cực tiểu tại x = 1 và \({y_{CT}}\)= y(1) = 2

Cách tìm cực trị của hàm số

Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:

Nếu f’(x) < 0 \(\forall x \in \left( {a;{x_0}} \right)\) và f’(x) > 0 \(\forall x \in \left( {{x_0};b} \right)\) thì \({x_0}\) là một điểm cực tiểu của hàm số f(x)
Nếu f’(x) > 0 \(\forall x \in \left( {a;{x_0}} \right)\) và f’(x) < 0 \(\forall x \in \left( {{x_0};b} \right)\) thì \({x_0}\) là một điểm cực đại của hàm số f(x)

Ví dụ: Tìm cực trị của hàm số \(y = {x^3} - 6{x^2} + 9x + 30\).

Tập xác định của hàm số là R.

Ta có: \(y' = 3{x^2} - 12x + 9\); y’ = 0 \( \Leftrightarrow \)x = 1 hoặc x = 3.

BBT: