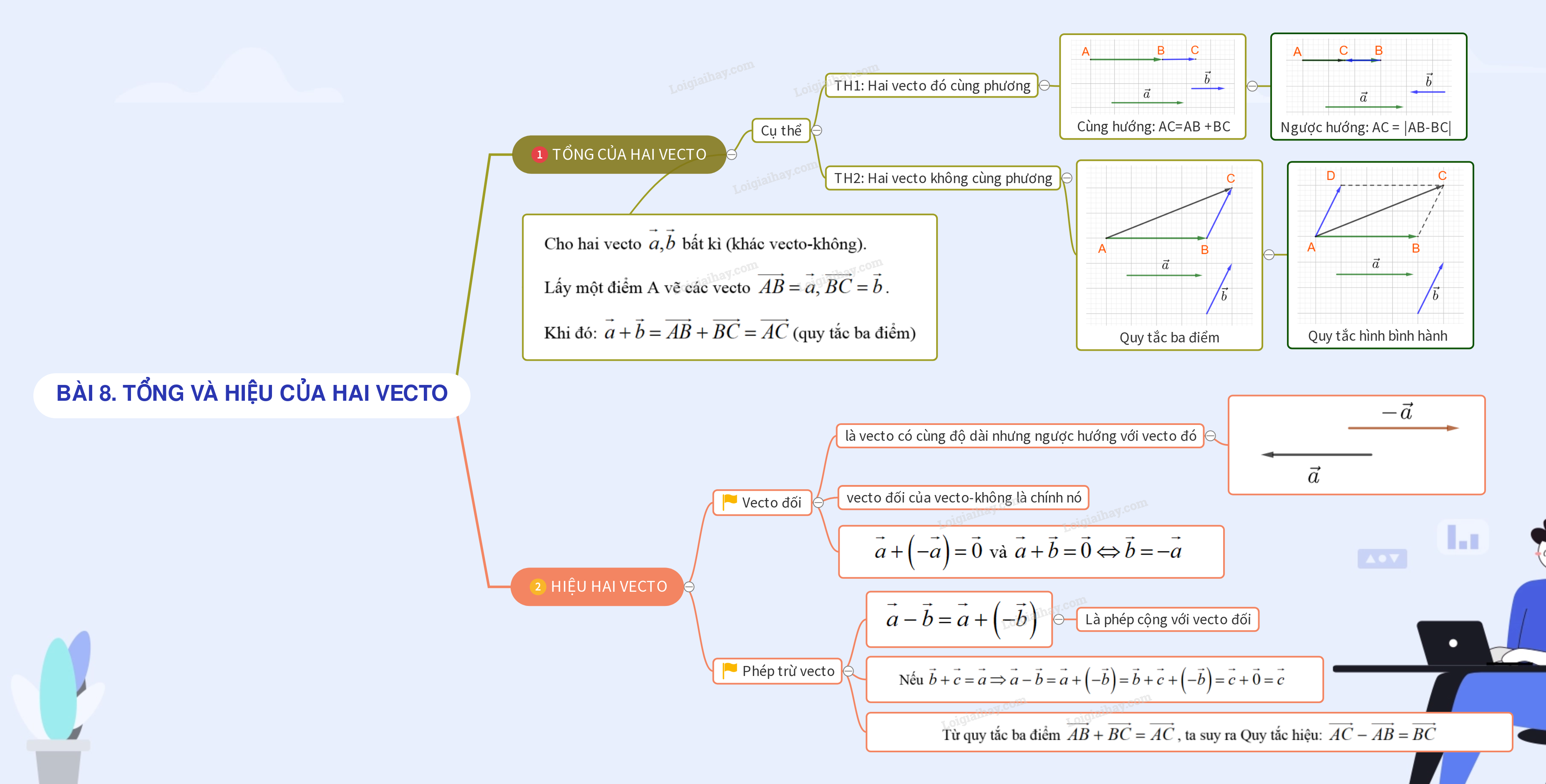
Lý thuyết Tổng và hiệu của hai vecto - SGK Toán 10 Kết nối tri thức
1. TỔNG CỦA HAI VECTƠ 2. HIỆU CỦA HAI VECTƠ
1. TỔNG CỦA HAI VECTƠ
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì (khác vecto-không). Lấy một điểm A vẽ các vecto \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \).
Khi đó: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)(quy tắc ba điểm)
a) Tổng hai vecto cùng phương \(\overrightarrow a ,\overrightarrow b \)
+) TH1: hai vecto \(\overrightarrow a ,\overrightarrow b \) cùng hướng: AC = AB + BC
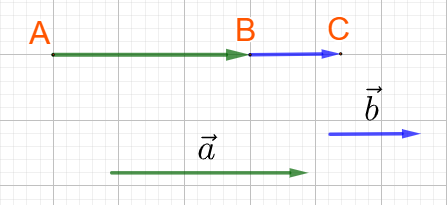
+) TH2: hai vecto \(\overrightarrow a ,\overrightarrow b \) ngược hướng: AC = |AB – BC|
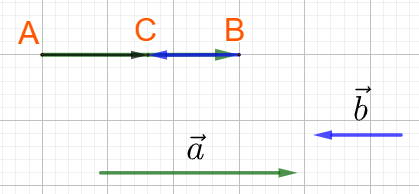
b) Tổng hai vecto không cùng phương
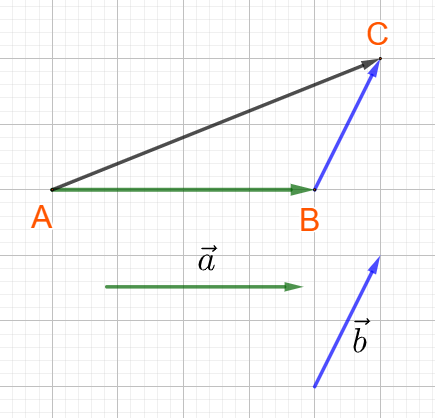
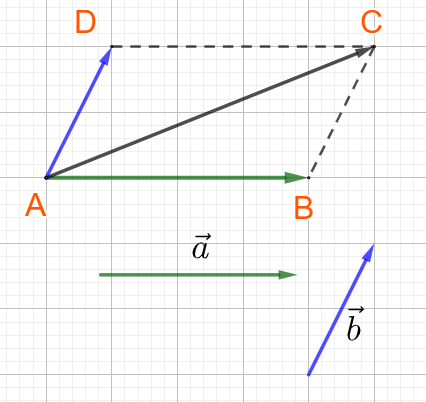
Nhận xét: vecto \(\overrightarrow {AC} \) là đường chéo của hình bình hành ABCD.
Do \(\overrightarrow {BC} = \overrightarrow {AD} \). Ta viết: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)( quy tắc hình bình hành )
2. HIỆU CỦA HAI VECTƠ
+) Vecto đối của vecto \(\overrightarrow a \): là vecto có cùng độ dài nhưng ngược hướng với vecto\(\overrightarrow a \).
Kí hiệu: \( - \;\overrightarrow a \)
Đặc biệt: Vecto đối của vecto \(\overrightarrow 0 \) là chính nó.
Chú ý: \(\overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0 \) và \(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow b = - \overrightarrow a \)
+) Phép trừ vecto: \(\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right)\)
Chú ý: Nếu \(\overrightarrow b + \overrightarrow c = \overrightarrow a \Rightarrow \overrightarrow a - \overrightarrow b = \overrightarrow c \)
Từ quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \), ta suy ra:
\( \Rightarrow \overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {BC} \) ( quy tắc hiệu )
Từ quy tắc ba điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \), ta suy ra Quy tắc hiệu : \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {BC} \)