Lý thuyết Vecto trong mặt phẳng tọa độ - SGK Toán 10 Kết nối tri thức
1. TỌA ĐỘ CỦA MỘT VECTO 2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
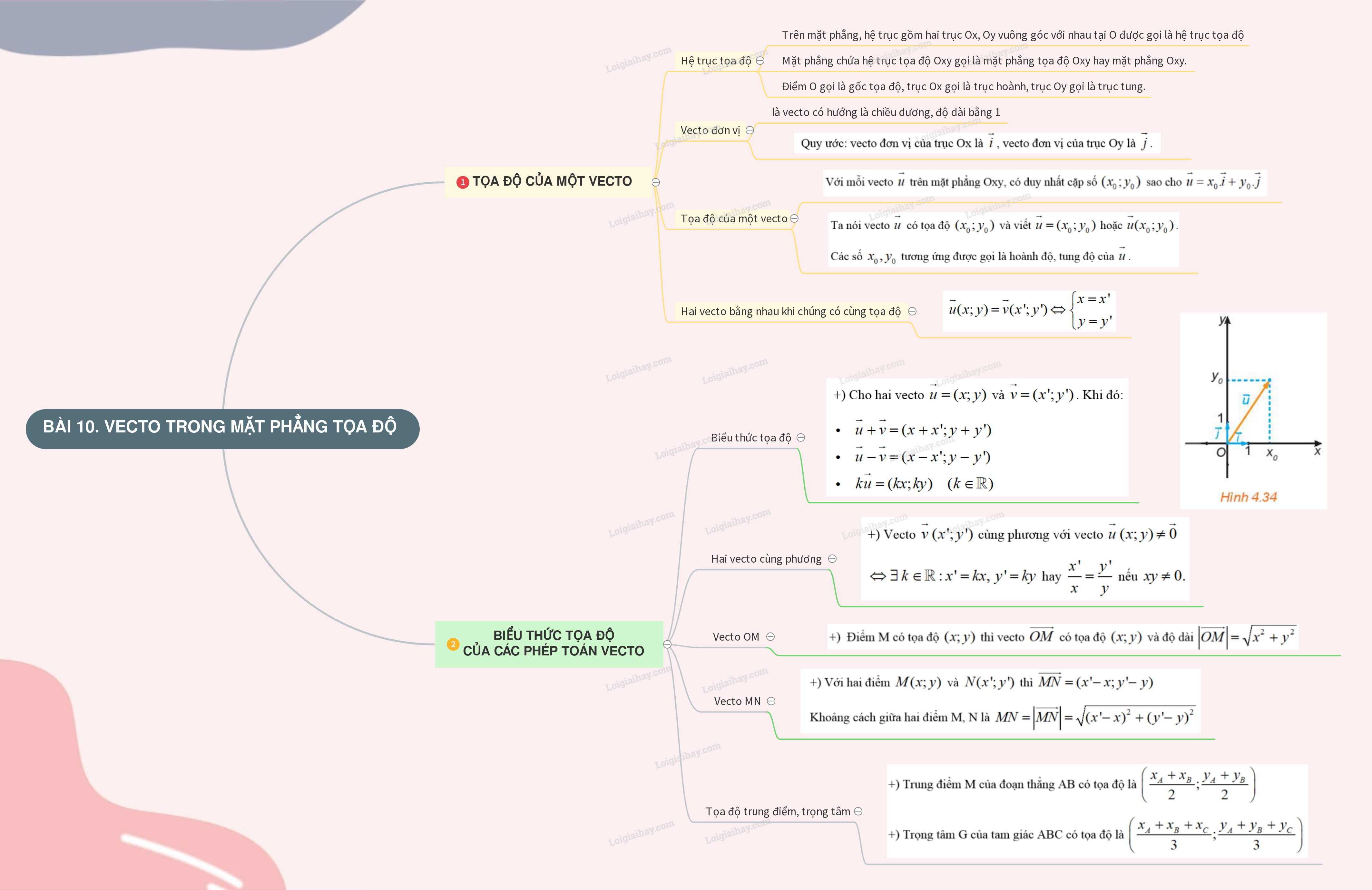
1. TỌA ĐỘ CỦA MỘT VECTO
+) Trên mặt phẳng, hệ trục gồm hai trục Ox, Oy vuông góc với nhau tại O được gọi là hệ trục tọa độ .
Mặt phẳng chứa hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy hay mặt phẳng Oxy .
+) Vecto đơn vị là vecto hướng là chiều dương, có độ dài bằng 1.
Quy ước : vecto đơn vị của trục Ox là \(\overrightarrow i \), vecto đơn vị của trục Oy là \(\overrightarrow j \). Điểm O gọi là gốc tọa độ , trục Ox gọi là trục hoành , trục Oy gọi là trục tung .

+) Với mỗi vecto \(\overrightarrow u \) trên mặt phẳng Oxy, có duy nhất cặp số \(({x_0};{y_0})\) sao cho \(\overrightarrow u = {x_0}.\overrightarrow i + {y_0}.\overrightarrow j \)
Ta nói vecto \(\overrightarrow u \) có tọa độ \(({x_0};{y_0})\) và viết \(\overrightarrow u = ({x_0};{y_0})\) hoặc \(\overrightarrow u ({x_0};{y_0})\).
Các số \({x_0},{y_0}\) tương ứng được gọi là hoành độ, tung độ của \(\overrightarrow u \).
+) Hai vecto bằng nhau khi và chỉ khi chúng có cùng tọa độ
\(\overrightarrow u (x;y) = \overrightarrow v (x';y') \Leftrightarrow \left\{ \begin{array}{l}x = x'\\y = y'\end{array} \right.\)
2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTO
+) Cho hai vecto \(\overrightarrow u = (x;y)\) và \(\overrightarrow v = (x';y')\). Khi đó:
\(\begin{array}{l}\overrightarrow u + \overrightarrow v = (x + x';y + y')\\\overrightarrow u - \overrightarrow v = (x - x';y - y')\\k\overrightarrow u = (kx;ky)\quad (k \in \mathbb{R})\end{array}\)
+) Vecto \(\overrightarrow v \;(x';y')\) cùng phương với vecto \(\overrightarrow u \;(x;y) \ne \overrightarrow 0 \)
\( \Leftrightarrow \exists \;k \in \mathbb{R}:x' = kx,\;y' = ky\) hay \(\frac{{x'}}{x} = \frac{{y'}}{y}\) nếu \(xy \ne 0.\)
+) Điểm M có tọa độ \((x;y)\) thì vecto \(\overrightarrow {OM} \) có tọa độ \((x;y)\) và độ dài \(\left| {\overrightarrow {OM} } \right| = \sqrt {{x^2} + {y^2}} \)
+) Với hai điểm \(M(x;y)\) và \(N(x';y')\) thì \(\overrightarrow {MN} = (x' - x;y' - y)\)
Khoảng cách giữa hai điểm M, N là \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{(x' - x)}^2} + {{(y' - y)}^2}} \)
+) Trung điểm M của đoạn thẳng AB có tọa độ là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
+) Trọng tâm G của tam giác ABC có tọa độ là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)