Lý thuyết về ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời.
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp.
1. Xác định chiều cao
a) Nhiệm vụ
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp.
b) Chuẩn bị
Giác kế, thước cuộn, máy tính bỏ túi (hoặc bảng lượng giác).
c) Hướng dẫn thực hiện (h.34)
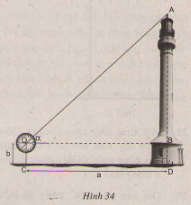
Đặt kế giác thẳng đứng cách chân tháp một khoảng a (CD=a), giả sử chiều cao của giác kế là b (OC=b).
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số đo \(\alpha\) của góc AOB.
Dùng bảng lượng giác hoặc máy tính bỏ túi để tính \(tg\alpha\). Tính tổng \(b+a\cdot tg\alpha\) và báo kết quả.
2. Xác định khoảng cách
a) Nhiệm vụ
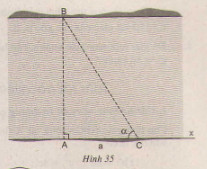
Xác định chiều rộng của một khúc sông mà việc đo đạc chỉ tiến hành tại một bờ sông.
b) Chuẩn bị
Ê-ke đạc, giác kế, thước cuộn, máy tính bỏ túi hoặc bảng lượng giác.
c) Hướng dẫn thực hiện
Ta có hai bờ sông song song với nhau.
Chọn một điểm B phía bên kia sông. Lấy một điểm A bên này sông sao cho vuông góc với các bờ sông.
Dùng ê-ke đạc kẻ đường thẳng Ax phía bên này sông sao cho \(Ax\perp AB\).
Lấy điểm C trên Ax, giả sử AC=a. Dùng giác kế đo góc ACB, giả sử
\(\widehat{ACB}=\alpha\).
Dùng máy tính bỏ túi hoặc bảng lượng giác để tính \(tg\alpha\) .
Tính tích \(a\cdot tg\alpha\) và báo kết quả.