Lý thuyết về đường kính và dây của đường tròn
Lý thuyết về đường kính và dây của đường tròn.
1. So sánh độ dài của đường kính và dây.
Định lý:
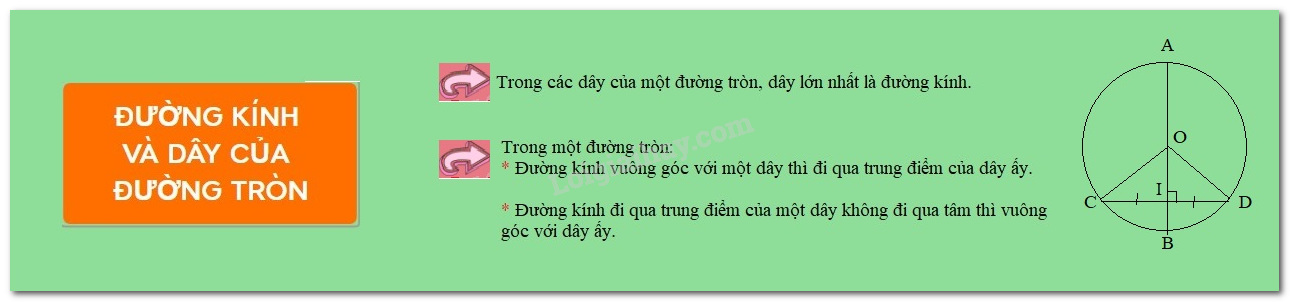
Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Xét đường tròn \(\left( {O,R} \right):A \in \left( O \right),B \in \left( O \right) \Rightarrow AB \le 2R\)
2. Quan hệ vuông góc giữa đường kính và dây.
Định lý 1:
- Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
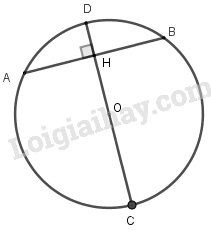
Xét \((O,R)\):
\(CD\) là đường kính
\(AB\) là dây cung
\(CD \bot AB\) tại \(H\)
\(=> H\) là trung điểm của \(AB\)
Định lý 2: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
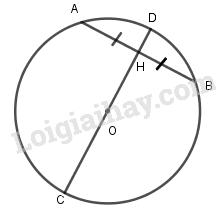
Xét \((O,R)\):
\(CD\) là đường kính
\(AB\) là dây cung, \(O \notin AB\)
\( H\) là trung điểm của \(AB\), \(H \in CD\)
\(=> \) \(CD \bot AB\) tại \(H\)
3. Các dạng toán thường gặp
Tính độ dài đoạn thẳng và các yếu tố liên quan.
Phương pháp:
Ta thường sử dụng các kiến thức sau:
+) Quan hệ vuông góc giữa đường kính và dây
Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Dùng định lý Pytago, hệ thức lượng trong tam giác vuông.