Lý thuyết đồ thị của hàm số y = ax + b (a ≠ 0).
Đồ thị của hàm số y = ax + b
1. Đồ thị hàm số \(y = ax + b\, (a ≠ 0).\)
Đồ thị của hàm số \(y = ax + b \,(a ≠ 0)\) là một đường thẳng:
+) Cắt trục tung tại điểm có tung độ bằng \(b;\)
+) Song song với đường thẳng \(y = ax\) nếu \(b ≠ 0\) và trùng với đường thẳng \(y = ax\) nếu \(b = 0.\)
Đồ thị này cũng được gọi là đường thẳng \(y = ax + b\) và \(b\) được gọi là tung độ gốc của đường thẳng.
Lưu ý: Đồ thị hàm số \(y = ax + b\) cắt trục hoành tại điểm \(Q\left( { - \dfrac{b}{a};0} \right).\)
2. Cách vẽ đồ thị của hàm số \(y = ax + b (a ≠ 0).\)
- Chọn điểm \(P(0; b)\) (trên trục \(Oy\)).
- Chọn điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) (trên trục \(Ox\)).
- Kẻ đường thẳng \(PQ\) ta được đồ thị của hàm số \(y=ax+b.\)
Lưu ý:
+ Vì đồ thị \(y = ax + b (a ≠ 0)\) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
+ Trong trường hợp giá trị \(- \dfrac{b}{a}\) khó xác định trên trục Ox thì ta có thể thay điểm Q bằng cách chọn một giá trị \(x_1\) của \(x\) sao cho điểm \(Q'(x_1, y_1 )\) (trong đó \(y_1 = ax_1 + b\)) dễ xác định hơn trong mặt phẳng tọa độ.
Ví dụ:
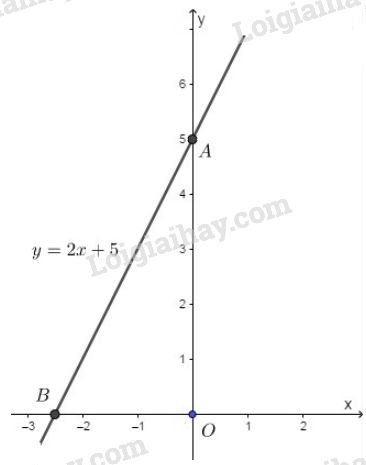
Vẽ đồ thị hàm số \(y = 2x + 5\).
+ Cho \(x = 0 \Rightarrow y = 2.0 +5=5 \Rightarrow A(0; 5)\)
+ Cho \(y=0 \Rightarrow 0= 2. x +5 \Rightarrow x=\dfrac{-5}{2}\)\( \Rightarrow B {\left(-\dfrac{5}{2}; 0 \right)}\)
Do đó đồ thị hàm số là đường thẳng đi qua hai điểm \(A(0; 5)\) và \(B \left( { - \dfrac{5}{2};0} \right)\).
3. Các dạng toán cơ bản
Dạng 1: Vẽ và nhận dạng đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$
Phương pháp:
Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng
Trường hợp 1: Nếu \(b = 0\) ta có hàm số \(y = ax\) . Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a).\)
Trường hợp 2: Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Dạng 2: Tìm tọa độ giao điểm của hai đường thẳng
Phương pháp:
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
Ví dụ: Tìm tọa độ giao điểm của hai đường thẳng \(y = 2x + 1\) và \(y=x+2\)
Xét phương trình hoành độ giao điểm của hai đường thẳng ta có:
\(\begin{array}{l} 2x + 1 = x + 2\\ \Leftrightarrow 2x - x = 2 - 1\\ \Leftrightarrow x = 1\\ \Rightarrow y = x + 2 = 1 + 2 = 3 \end{array}\)
Vậy tọa độ giao điểm cần tìm là: \((1;3)\)
Dạng 3: Xác định hệ số a,b để đồ thị hàm số \(y = ax + b\,(a \ne 0)\) cắt trục \(Ox,Oy\) hay đi qua một điểm nào đó.
Phương pháp:
Ta sử dụng kiến thức: Đồ thị hàm số \(y = ax + b\,(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b\).
Ví dụ:
Biết rằng đồ thị của hàm số \(y = ax + 2\) đi qua điểm \(A (-1; 3)\). Tìm a.
Thay \(x=-1;y=3\) vào hàm số \(y = ax + 2\) ta được: \(3 = - 1.a + 2 \Leftrightarrow a = - 1\)
Vậy \(a=-1\)
Dạng 4: Tính đồng quy của ba đường thẳng
Phương pháp:
Để xét tính đồng quy của ba đường thẳng cho trước, ta thực hiện các bước sau
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.
Bước 2. Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thằng còn lại thì kết luận ba đường thẳng đó đồng quy.
