Lý thuyết. Hình cầu. Diện tích hình cầu và thể tích hình cầu
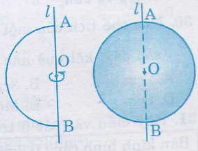
Khi quay nửa hình tròn tâp O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.
1. Hình cầu
Khi quay nửa hình tròn tâm \(O\), bán kính \(R\) một vòng quanh đường kính \(AB\) cố định thì được một hình cầu.
- Điểm \(O\) được gọi là tâm, độ dài \(R\) là bán kính của hình cầu.
- Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu
2. Diện tích mặt cầu
Công thức diện tích mặt cầu: \(S = 4\pi {R^2} = \pi {d^2}\)
\(R\) là bán kính, \(d\) là đường kính mặt cầu.
3. Thể tích hình cầu
Thể tích hình cầu bán kính \(R\) : \(\displaystyle V ={4 \over 3}\pi {R^3}\)
Cùng chủ đề:
Lý thuyết. Hình cầu. Diện tích hình cầu và thể tích hình cầu