Lý thuyết Đồ thị của hàm số y = ax^2 (a ≠ 0).
Đồ thị của hàm số
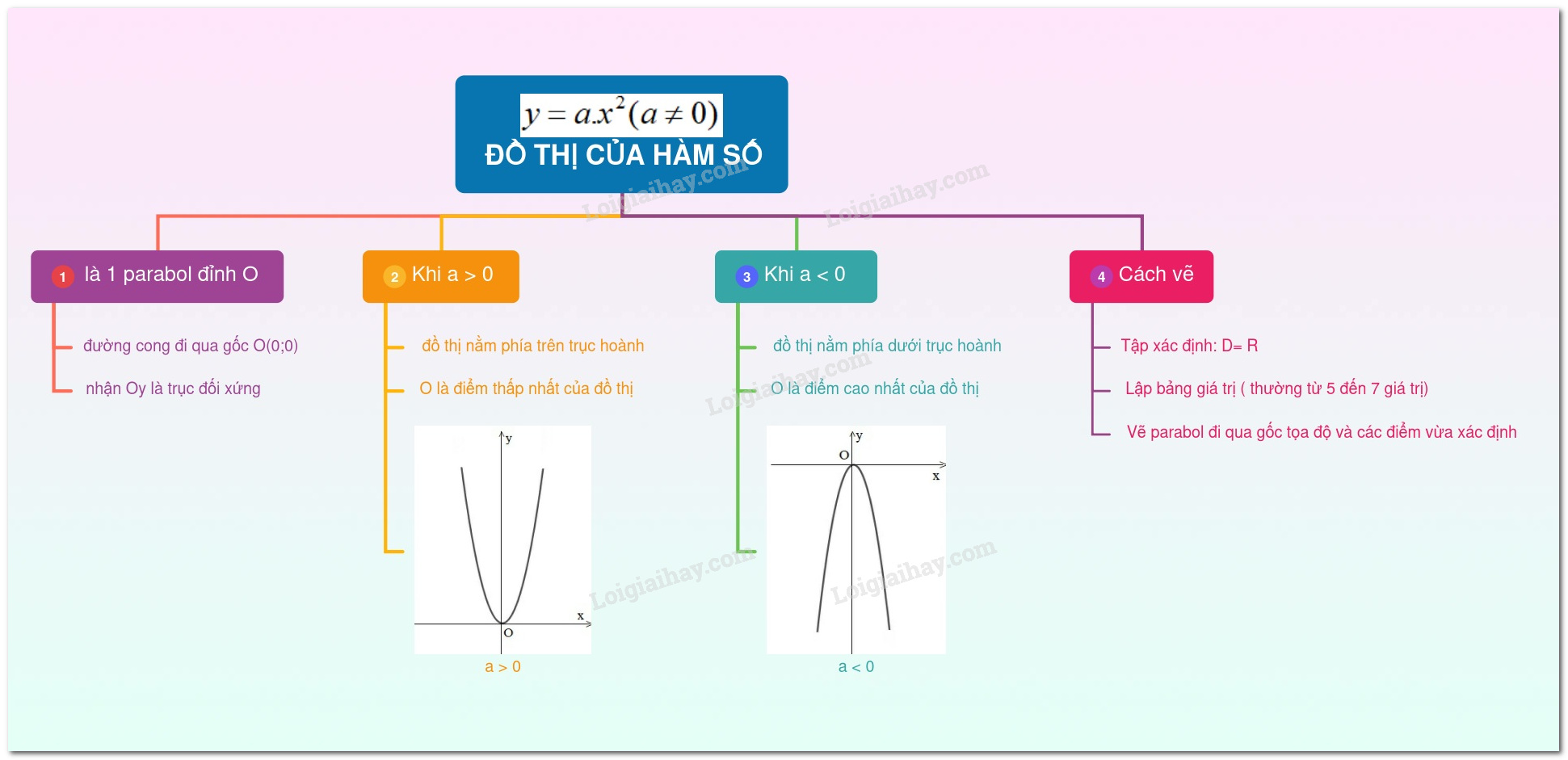
1. Đồ thị hàm số
Đồ thị của hàm số \(y = a{x^2}\) (\(a ≠ 0\)) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
2. Cách vẽ đồ thị
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ \(5\) đến \(7\) giá trị) tương ứng giữa \(x\) và \(y.\)
Bước 3: Vẽ đồ thị và kết luận.
Cùng chủ đề:
Lý thuyết Đồ thị của hàm số y = ax^2 (a ≠ 0)