Toán lớp 4 trang 28 - Bài 64: Luyện tập chung - SGK Cánh diều
Nêu phân số chỉ phân số đã tô màu trong mỗi hình sau: a) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):
Câu 1
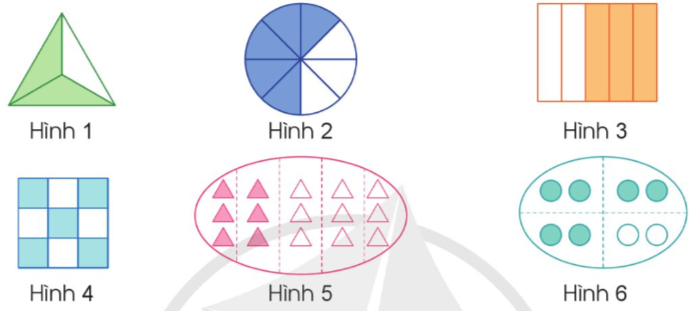
Nêu phân số chỉ số phần đã tô màu trong mỗi hình sau:
Phương pháp giải:
Phân số chỉ số phần đã tô màu có tử số là số phần tô màu, mẫu số là số phần bằng nhau của hình đó.
Lời giải chi tiết:
Hình 1: $\frac{2}{3}$ ; Hình 2: $\frac{5}{8}$
Hình 3: $\frac{3}{5}$ ; Hình 4: $\frac{5}{9}$
Hình 5: $\frac{2}{5}$ ; Hình 6: $\frac{3}{4}$
Câu 2
a) Viết thương của mỗi phép chia sau dưới dạng phân số (theo mẫu):

b) Viết các số sau dưới dạng phân số có mẫu số là 1:

Phương pháp giải:
a) Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.
b) Mọi số tự nhiên có thể viết thành một phân số có tử số là số tự nhiên đó và mẫu số bằng 1.
Lời giải chi tiết:
a) 3 : 8 = $\frac{3}{8}$ ; 8 : 9 = $\frac{8}{9}$
4 : 7 = $\frac{4}{7}$ ; 12 : 5 = $\frac{{12}}{5}$
b) $7 = \frac{7}{1}$ ; $9 = \frac{9}{1}$ ; $21 = \frac{{21}}{1}$ ; $40 = \frac{{40}}{1}$
Câu 3
Quan sát hình vẽ, nêu phân số thích hợp:

Phương pháp giải:
Quan sát hình vẽ rồi viết phân số bằng phân số đã cho.
Lời giải chi tiết:
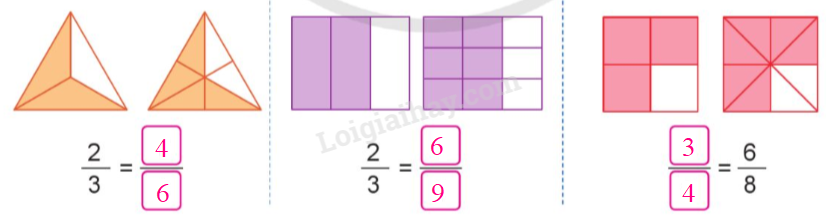
Câu 4
Trong các phân số $\frac{1}{4};\,\,\frac{6}{5};\,\,\frac{4}{{10}};\,\,\frac{{16}}{9};\,\,\frac{{10}}{{20}};\,\,\frac{8}{{18}}$
a) Phân số nào là phân số tối giản?
b) Rút gọn các phân số chưa tối giản
Phương pháp giải:
- Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1
- Cách rút gọn phân số:
+ Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
+ Chia tử số và mẫy số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) Các phân số tối giản là $\frac{1}{4};\,\,\frac{6}{5};\,\,\frac{{16}}{9}$
b) Các phân số chưa tối giản là $\frac{4}{{10}};\,\,\frac{{10}}{{20}};\,\,\frac{8}{{18}}$
$\frac{4}{{10}} = \frac{{4:2}}{{10:2}} = \frac{2}{5}$
$\frac{{10}}{{20}} = \frac{{10:10}}{{20:10}} = \frac{1}{2}$
$\frac{8}{{18}} = \frac{{8:2}}{{18:2}} = \frac{4}{9}$
Câu 5
Quy đồng mẫu số hai phân số:

Phương pháp giải:
- Tìm mẫu số chung - Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) Ta có: $\frac{8}{5} = \frac{{8 \times 2}}{{5 \times 2}} = \frac{{16}}{{10}}$ ; Giữ nguyên phân số $\frac{3}{{10}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{{10}}$ và $\frac{8}{5}$ ta được hai phân số $\frac{3}{{10}}$ và $\frac{{16}}{{10}}$
b) $\frac{4}{3} = \frac{{4 \times 2}}{{3 \times 2}} = \frac{8}{6}$ ; Giữ nguyên phân số $\frac{7}{6}$
Vậy quy đồng mẫu số hai phân số $\frac{4}{3}$ và $\frac{7}{6}$ ta được hai phân số $\frac{8}{6}$ và $\frac{7}{6}$
c) $\frac{3}{8} = \frac{{3 \times 8}}{{8 \times 8}} = \frac{{24}}{{64}}$ ; Giữ nguyên phân số $\frac{5}{{64}}$
Vậy quy đồng mẫu số hai phân số $\frac{3}{8}$ và $\frac{5}{{64}}$ ta được hai phân số $\frac{{24}}{{64}}$ và $\frac{5}{{64}}$
Câu 6
a)

b) Viết các phân số sau theo thứ tự từ lớn đến bé:

Phương pháp giải:
a) Muốn so sánh các phân số khác mẫu số, ta có thể quy đồng mẫu số các phân số đó, rồi so sánh các tử số của phân số mới.
b) So sánh các phân số rồi sắp xếp theo thứ tự từ lớn đến bé
Lời giải chi tiết:
a)
+) $\frac{5}{6} < \frac{7}{6}$
+) 2 = $\frac{6}{3}$
+) $\frac{3}{7}$ và $\frac{4}{{14}}$
Ta có: $\frac{3}{7} = \frac{{3 \times 2}}{{7 \times 2}} = \frac{6}{{14}}$
Vì $\frac{6}{{14}} > \frac{4}{{14}}$ nên $\frac{3}{7} > \frac{4}{{14}}$
+) $\frac{{12}}{{20}}$ và $\frac{4}{5}$
Ta có: $\frac{4}{5} = \frac{{4 \times 4}}{{5 \times 4}} = \frac{{16}}{{20}}$ ; Giữ nguyên phân số: $\frac{{12}}{{20}}$
Vì $\frac{{12}}{{20}}$ < $\frac{{16}}{{20}}$ nên $\frac{{12}}{{20}}$ < $\frac{4}{5}$
Vậy ta có kết quả như sau:
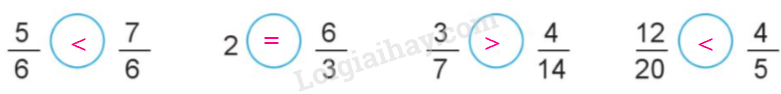
b) Quy đồng ba phân số$\frac{1}{{13}};\,\,\frac{{25}}{{13}};\,\,\frac{4}{{39}}$
$\frac{1}{{13}} = \frac{{1 \times 3}}{{13 \times 3}} = \frac{3}{{39}}$
$\frac{{25}}{{13}} = \frac{{25 \times 3}}{{13 \times 3}} = \frac{{75}}{{39}}$ ; Giữ nguyên phân số $\frac{4}{{39}}$
Vì $\frac{{75}}{{39}} > \frac{4}{{39}} > \frac{3}{{39}}$ nên $\frac{{25}}{{13}} > \frac{4}{{39}} > \frac{1}{{13}}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{{25}}{{13}};\,\,\frac{4}{{39}};\,\,\frac{1}{{13}}$
Quy đồng ba phân số $\frac{2}{8};\,\,\frac{7}{4};\,\,\frac{9}{{16}}$
$\frac{2}{8} = \frac{{2 \times 2}}{{8 \times 2}} = \frac{4}{{16}}$
$\frac{7}{4} = \frac{{7 \times 4}}{{4 \times 4}} = \frac{{28}}{{16}}$ ; Giữ nguyên phân số $\frac{9}{{16}}$
Vì $\frac{{28}}{{16}} > \frac{9}{{16}} > \frac{4}{{16}}$ nên $\frac{7}{4} > \frac{9}{{16}} > \frac{2}{8}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{7}{4};\,\,\frac{9}{{16}};\,\,\frac{2}{8}$
Câu 7
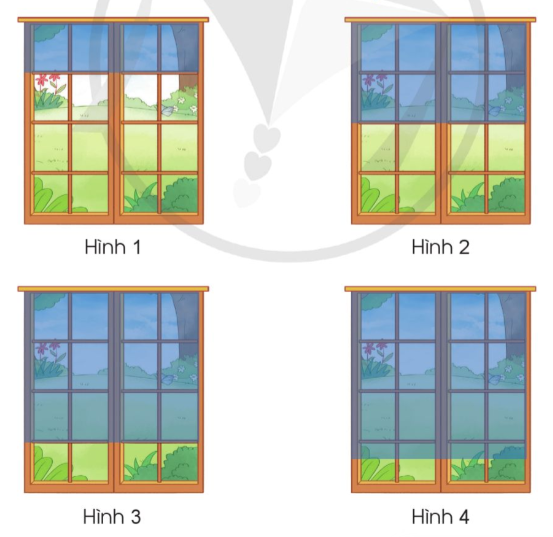
Bức rèm trong hình vẽ nào dưới đây che $\frac{3}{4}$ cửa sổ?
Phương pháp giải:
Quan sát rồi tìm hình vẽ có bức rèm che $\frac{3}{4}$ cửa sổ.
Lời giải chi tiết:
Bức rèm ở hình 3 che $\frac{3}{4}$ cửa sổ.