Toán lớp 4 trang 26 - Bài 63: Luyện tập - SGK Cánh diều — Không quảng cáo

Câu 1

So sánh hai phân số:

Phương pháp giải:

Trong hai phân số có cùng mẫu số:

- Phân số nào có tử số bé hơn thì bé hơn

- Phân số nào có tử số lớn hơn thì lớn hơn

- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Lời giải chi tiết:

a) $\frac{5}{9} < \frac{7}{9}$

b) $\frac{7}{6} > \frac{6}{6}$

c) $\frac{3}{{14}} < \frac{5}{{14}}$

d) $\frac{5}{8} < \frac{9}{8}$

Câu 2

Quy đồng mẫu số rồi so sánh hai phân số:

a) $\frac{2}{5}$ và $\frac{3}{{10}}$

b) $\frac{7}{{12}}$ và $\frac{5}{6}$

c) $\frac{3}{4}$ và $\frac{1}{2}$

d) $\frac{8}{3}$ và $\frac{{11}}{{21}}$

Phương pháp giải:

- Quy đồng mẫu số:

+ Tìm mẫu số chung + Tìm thương của mẫu số chung và mẫu số của phân số cần quy đồng

+ Nhân cả tử số và mẫu số của phân số với thương vừa tìm được

- So sánh hai phân số cùng mẫu số

Lời giải chi tiết:

a) $\frac{2}{5} = \frac{{2 \times 2}}{{5 \times 2}} = \frac{4}{{10}}$, giữ nguyên phân số $\frac{3}{{10}}$

Vì $\frac{4}{{10}}$ > $\frac{3}{{10}}$ nên $\frac{2}{5}$ > $\frac{3}{{10}}$

b) $\frac{5}{6} = \frac{{5 \times 2}}{{6 \times 2}} = \frac{{10}}{{12}}$ ; giữ nguyên phân số $\frac{7}{{12}}$

Vì $\frac{7}{{12}}$ < $\frac{{10}}{{12}}$ nên $\frac{7}{{12}}$ < $\frac{5}{6}$

c) $\frac{1}{2} = \frac{{1 \times 2}}{{2 \times 2}} = \frac{2}{4}$ ; giữ nguyên phân số $\frac{3}{4}$

Vì $\frac{3}{4}$> $\frac{2}{4}$ nên $\frac{3}{4}$ > $\frac{1}{2}$

d) $\frac{8}{3} = \frac{{8 \times 7}}{{3 \times 7}} = \frac{{56}}{{21}}$ ; giữ nguyên phân số $\frac{{11}}{{21}}$

Vì $\frac{{56}}{{21}}$ > $\frac{{11}}{{21}}$ nên $\frac{8}{3}$ > $\frac{{11}}{{21}}$

Câu 3

a) >, <, = ?

b) Viết các số sau theo thứ tự từ bé đến lớn:

Phương pháp giải:

a)

+ Nếu tử số bé hơn mẫu số thì phân số bé hơn 1

+ Nếu tử số lớn hơn mẫu số thì phân số lớn hơn 1

+ Nếu tử số bằng mẫu số thì phân số bằng 1.

b) So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn

Lời giải chi tiết:

a) $\frac{5}{9}$ < 1

$\frac{8}{7}$ > 1

$\frac{9}{9}$ = 1

$\frac{9}{2}$ và $\frac{3}{4}$

Ta có $\frac{9}{2}$= $\frac{{9 \times 2}}{{2 \times 2}} = \frac{{18}}{4}$

Vì $\frac{{18}}{4}$ > $\frac{3}{4}$nên  $\frac{9}{2}$ > $\frac{3}{4}$

b)

+) $\frac{3}{5};\,\,\frac{8}{5}$ và $\frac{2}{5}$

Ta có $\frac{2}{5} < \frac{3}{5} < \frac{8}{5}$ .Vậy các phân số đã cho xếp theo thứ tự từ bé đến lớn là $\frac{2}{5};\,\,\,\frac{3}{5};\,\,\,\frac{8}{5}$

+) $\frac{5}{2};\,\,\frac{1}{6}$ và 1

Ta có $\frac{5}{2} > 1$ ; $\frac{1}{6} < 1$

Vậy các phân số đã cho xếp theo thứ tự từ bé đến lớn là: $\frac{1}{6};\,\,\,1\,\,;\,\,\,\frac{5}{2}$

Câu 4

a) Xếp các thẻ ghi phân số vào vị trí thích hợp trên tia số:

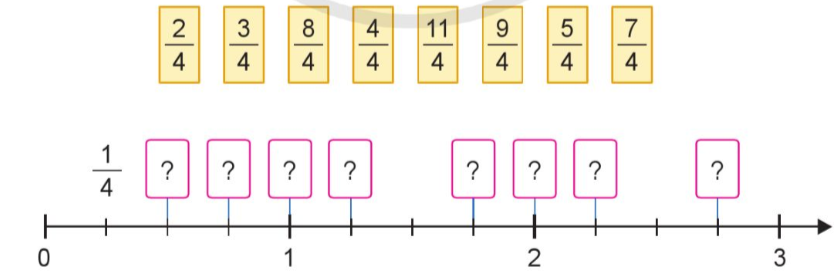
b) Trong các phân số ở câu a, phân số nào bé hơn 1? Phân số nào lớn hơn 1?

Phương pháp giải:

a) Xếp các thẻ ghi phân số vào vị trí thích hợp trên tia số

b) Áp dụng phương pháp so sánh phân số với 1

+ Nếu tử số bé hơn mẫu số thì phân số bé hơn 1

+ Nếu tử số lớn hơn mẫu số thì phân số lớn hơn 1

Lời giải chi tiết:

a)

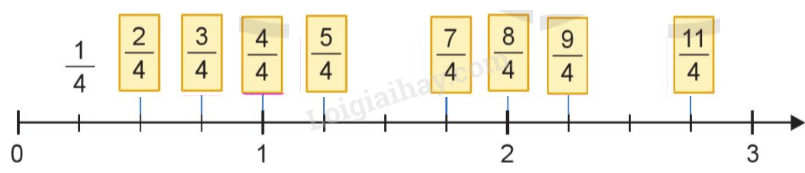
b) Các phân số bé hơn 1 là: $\frac{1}{4};{\mkern 1mu} {\mkern 1mu} \frac{2}{4}{\mkern 1mu} {\mkern 1mu} ;{\mkern 1mu} {\mkern 1mu} \frac{3}{4}{\mkern 1mu} {\text{ }}$

Các phân số lớn hơn 1 là: $\frac{5}{4};\,\,\frac{7}{4};\,\,\frac{8}{4};\,\,\frac{9}{4};\,\,\,\frac{{11}}{4}$

Câu 5

Linh, Nguyên, Khôi đọc ba quyển sách giống nhau.

a) Trong hai bạn Linh và Khôi, ai đã đọc được nhiều trang sách hơn?

b) Trong ba bạn, ai đã đọc được nhiều trang sách nhất?

Phương pháp giải:

a) Quy đồng mẫu số hai phân số $\frac{3}{4}$ và $\frac{5}{8}$ rồi so sánh và kết luận

b) Quy đồng mẫu số ba phân số $\frac{3}{4};\frac{1}{2};\frac{5}{8}$ rồi so sánh và kết luận

Lời giải chi tiết:

a) Ta có $\frac{3}{4} = \frac{{3 \times 2}}{{4 \times 2}} = \frac{6}{8}$; Giữ nguyên phân số $\frac{5}{8}$

Vì $\frac{6}{8} > \frac{5}{8}$ nên $\frac{3}{4}$ > $\frac{5}{8}$

Vậy bạn Linh đọc được nhiều trang sách hơn bạn Khôi.

b) Ta có $\frac{1}{2} = \frac{{1 \times 4}}{{2 \times 4}} = \frac{4}{8}$

Vì $\frac{4}{8} < \frac{5}{8} < \frac{6}{8}$ nên $\frac{1}{2} < \frac{5}{8} < \frac{3}{4}$

Vậy bạn Linh đã đọc được nhiều trang sách nhất.

Câu 6

Một số loại thức ăn chế biến từ đậu xanh, đậu tương thường có lợi cho sức khỏe, đem lại giá trị dinh dưỡng cao. Hãy so sánh hàm lượng protein (chất đạm) có trong 100 g của một loại đậu xanh và có trong 100g của một loại đậu tương như thông tin sau:

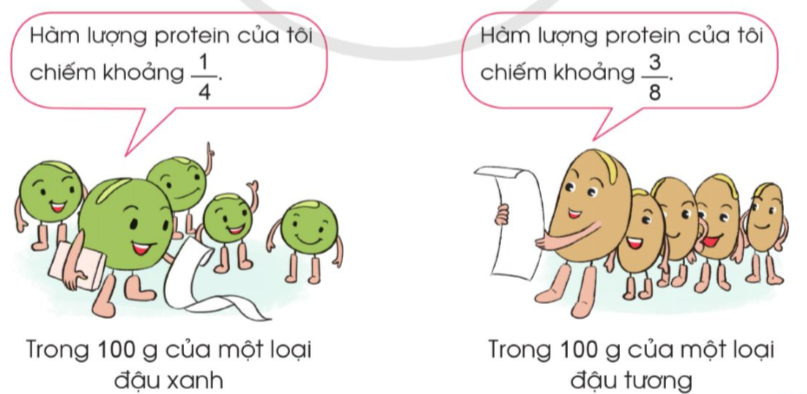
Phương pháp giải:

- Quy đồng mẫu số hai phân số $\frac{1}{4}$ và $\frac{3}{8}$

- So sánh hai phân số sau khi quy đồng và kết luận

Lời giải chi tiết:

Ta có: $\frac{1}{4} = \frac{{1 \times 2}}{{4 \times 2}} = \frac{2}{8}$; Giữ nguyên phân số $\frac{3}{8}$

Vì $\frac{2}{8} < \frac{3}{8}$ nên $\frac{1}{4}$ < $\frac{3}{8}$

Vậy hàm lượng protein (chất đạm) có trong 100 g của một loại đậu xanh ít hơn hàm lượng protein có trong 100g của một loại đậu tương.