Toán lớp 4 trang 51 - Bài 64: Em làm được những gì - SGK Chân trời sáng tạo
Viết phân số tối giản chỉ phần tô màu trong mỗi hình. Viết phân số có tử số là số tự nhiên lớn nhất có một chữ số, mẫu số là số tự nhiên bé nhất có hai chữ số
Câu 1
Số?

Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:

Câu 2
Rút gọn các phân số.

Phương pháp giải:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) $\frac{{35}}{{60}} = \frac{{35:5}}{{60:5}} = \frac{7}{{12}}$
b) $\frac{{14}}{{18}} = \frac{{14:2}}{{18:2}} = \frac{7}{9}$
c) $\frac{{15}}{{48}} = \frac{{15:3}}{{48:3}} = \frac{5}{{16}}$
d) $\frac{{27}}{{18}} = \frac{{27:9}}{{18:9}} = \frac{3}{2}$
e) $\frac{{90}}{{70}} = \frac{{90:10}}{{70:10}} = \frac{9}{7}$
Câu 3
Viết phân số tối giản chỉ phần tô màu trong mỗi hình.

Phương pháp giải:
- Viết phân số chỉ phần tô màu trong mỗi hình
- Rút gọn phân số
Lời giải chi tiết:
a) Đã tô màu $\frac{3}{{12}}$ hình a. Vậy phân số tối giản chỉ phần tô màu là $\frac{1}{4}$
b) Đã tô màu $\frac{4}{{12}}$ hình b. Vậy phân số tối giản chỉ phần tô màu là $\frac{1}{3}$
c) Đã tô màu $\frac{6}{{12}}$ hình c. Vậy phân số tối giản chỉ phần tô màu là $\frac{1}{2}$
d) Đã tô màu $\frac{8}{{12}}$ hình d. Vậy phân số tối giản chỉ phần tô màu là $\frac{2}{3}$
e) Đã tô màu $\frac{9}{{12}}$ hình e. Vậy phân số tối giản chỉ phần tô màu là $\frac{3}{4}$
Câu 4
Trong mỗi hình dưới đây, một số hình vẽ đã được tô màu:
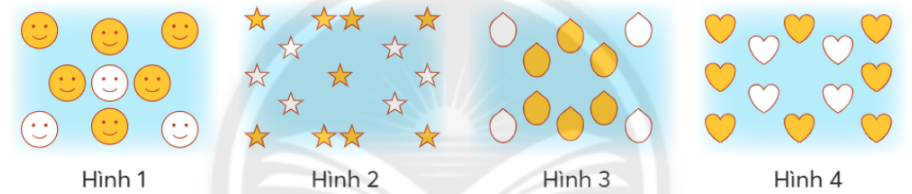
a) Viết phân số chỉ phần đã tô màu ở mỗi hình.
b) Rút gọn các phân số đó
Phương pháp giải:
a) Phân số chỉ phần đã tô màu ở mỗi hình có tử số là số phần được tô màu, mẫu số là số phần bằng nhau có trong hình đó.
b) - Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
a) Phân số chỉ phần đã tô màu ở mỗi hình là:

b) Rút gọn phân số:

Câu 5
Viết phân số có tử số là số tự nhiên lớn nhất có một chữ số, mẫu số là số tự nhiên bé nhất có hai chữ số. Phân số này có là phân số tối giản không? Tại sao?
Phương pháp giải:
- Viết phân số theo yêu cầu của bài toán
- Phân số tối giản là phân số mà tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1
Lời giải chi tiết:
Số tự nhiên lớn nhất có một chữ số là 9
Số tự nhiên bé nhất có hai chữ số là 10
Vậy phân số cần tìm là $\frac{9}{{10}}$.
Phân số này có là phân số tối giản vì tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
Câu 6
Các phân số sau có bằng nhau không? Tại sao?
$\frac{4}{6}$ ; $\frac{8}{{12}}$ ; $\frac{{10}}{{15}}$ ; $\frac{{14}}{{21}}$
Phương pháp giải:
Rút gọn các phân số rồi kết luận các phân số đã cho có bằng nhau không.
Lời giải chi tiết:
$\frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}$ ; $\frac{8}{{12}} = \frac{{8:4}}{{12:4}} = \frac{2}{3}$
$\frac{{10}}{{15}} = \frac{{10:5}}{{15:5}} = \frac{2}{3}$ ; $\frac{{14}}{{21}} = \frac{{14:7}}{{21:7}} = \frac{2}{3}$
Vậy các phân số đã cho bằng nhau.
Thử thách
Trong hình vẽ dưới đây, từ lúc 8 giờ, kim phút mỗi đồng hồ đã di chuyển trong khoảng thời gian bằng mấy phần của một giờ?
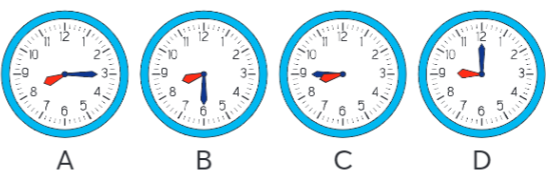
Phương pháp giải:
- Tìm số phút đồng hồ đã di chuyển từ lúc 8 giờ đến thời điểm hiện tại trên mỗi đồng hồ.
- Phân số cần tìm có tử số là khoảng thời gian di chuyển vừa tìm được, mẫu số là 60
- Rút gọn phân số
Lời giải chi tiết:
Hình A: Từ 8 giờ đến 8 giờ 15, kim phút di chuyển trong 15 phút.
Vậy kim phút đã di chuyển trong $\frac{{15}}{{60}} = \frac{1}{4}$ giờ.
Hình B : Từ 8 giờ đến 8 giờ 30 phút, kim phút đã di chuyển trong 30 phút
Vậy kim phút đã di chuyển trong $\frac{{30}}{{60}} = \frac{1}{2}$ giờ
Hình C: Từ 8 giờ đến 8 giờ 45 phút, kim phút đã di chuyển trong 45 phút
Vậy kim phút đã di chuyển trong $\frac{{45}}{{60}} = \frac{3}{4}$ giờ
Hình D : Từ 8 giờ đến 9 giờ, kim phút đã di chuyển trong 60 phút
Vậy kim phút đã di chuyển trong $\frac{{60}}{{60}} = 1$ giờ