Toán lớp 4 trang 62 - Bài 57: Quy đồng mẫu số các phân số - SGK Kết nối tri thức

Quy đồng mẫu số các phân số (theo mẫu) Rút gọn rồi quy đồng mẫu các số (theo mẫu)

Hoạt động Câu 1

Quy đồng mẫu số các phân số (theo mẫu).

Phương pháp giải:

- Xác định mẫu số chung.

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là mẫu số chung.

Lời giải chi tiết:

a) $\frac{5}{9}$ và $\frac{{11}}{{18}}$

$\frac{5}{9} = \frac{{5 \times 2}}{{9 \times 2}} = \frac{{10}}{{18}}$

b) $\frac{{13}}{{60}}$ và $\frac{9}{{20}}$

$\frac{9}{{20}} = \frac{{9 \times 3}}{{20 \times 3}} = \frac{{27}}{{60}}$

Hoạt động Câu 2

Tìm hai phân số lần lượt bằng $\frac{2}{3}$ ; $\frac{3}{4}$ và có mẫu số chung là 12.

Phương pháp giải:

Bước 1: Lấy mẫu số chung chia cho mẫu số của các phân số đã cho.

Bước 2: Nhân cả tử số và mẫu số của phân số đã cho với số vừa tìm được ở bước 1.

Lời giải chi tiết:

Ta có 12 : 3 = 4

$\frac{2}{3} = \frac{{2 \times 4}}{{3 \times 4}} = \frac{8}{{12}}$

Vậy phân số bằng $\frac{2}{3}$ và có mẫu số chung là 12 là $\frac{8}{{12}}$ Ta có 12 : 4 = 3

$\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$

Vậy phân số bằng $\frac{3}{4}$ và có mẫu số chung là 12 là $\frac{9}{{12}}$

Luyện tập Câu 1

Quy đồng mẫu số các phân số.

a) $\frac{5}{6}$ và $\frac{{11}}{{24}}$

b) $\frac{7}{{15}}$ và $\frac{{19}}{{45}}$

c) $\frac{2}{3}$ và $\frac{{77}}{{300}}$

Phương pháp giải:

- Xác định mẫu số chung.

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là mẫu số chung.

Lời giải chi tiết:

a) $\frac{5}{6}$ và $\frac{{11}}{{24}}$

$\frac{5}{6} = \frac{{5 \times 4}}{{6 \times 4}} = \frac{{20}}{{24}}$

b) $\frac{7}{{15}}$ và $\frac{{19}}{{45}}$

$\frac{7}{{15}} = \frac{{7 \times 3}}{{15 \times 3}} = \frac{{21}}{{45}}$

c) $\frac{2}{3}$ và $\frac{{77}}{{300}}$

$\frac{2}{3} = \frac{{2 \times 100}}{{3 \times 100}} = \frac{{200}}{{300}}$

Luyện tập Câu 2

Rút gọn rồi quy đồng mẫu số các phân số (theo mẫu).

Phương pháp giải:

Rút gọn phân số đến tối giản
Quy đồng mẫu số hai phân số:

- Xác định mẫu số chung.

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là mẫu số chung.

Lời giải chi tiết:

a) $\frac{2}{{36}} = \frac{1}{{18}}\,\,\,;\,\,\,\frac{8}{{12}} = \frac{2}{3}$

$\frac{2}{3} = \frac{{2 \times 6}}{{3 \times 6}} = \frac{{12}}{{18}}$

b) $\frac{{10}}{{25}} = \frac{2}{5}\,\,\,;\,\,\,\,\frac{{14}}{{40}} = \frac{7}{{20}}$

$\frac{2}{5} = \frac{{2 \times 4}}{{5 \times 4}} = \frac{8}{{20}}$

Luyện tập Câu 3

Quy đồng mẫu số các phân số (theo mẫu).

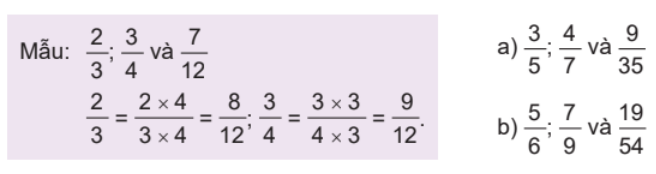
Phương pháp giải:

- Xác định mẫu số chung.

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số kia

Lời giải chi tiết:

a) $\frac{3}{5};\frac{4}{7}$ và $\frac{9}{{35}}$

$\frac{3}{5} = \frac{{3 \times 7}}{{5 \times 7}} = \frac{{21}}{{35}}\,\,\,\,;\,\,\,\,\,\frac{4}{7} = \frac{{4 \times 5}}{{7 \times 5}} = \frac{{20}}{{35}}$

b) $\frac{5}{6};\frac{7}{9}$ và $\frac{{19}}{{54}}$

$\frac{5}{6} = \frac{{5 \times 9}}{{6 \times 9}} = \frac{{45}}{{54}}\,\,\,\,\,;\,\,\,\,\,\,\frac{7}{9} = \frac{{7 \times 6}}{{9 \times 6}} = \frac{{42}}{{54}}$