Trả lời câu hỏi Bài 3 trang 15 Toán 9 Tập 2
Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm.
Đề bài
Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm.
\(\left( {III} \right)\left\{ \matrix{4x - 2y = - 6 \hfill \cr - 2x + y = 3 \hfill \cr} \right.\)
Phương pháp giải - Xem chi tiết
Xét hệ hai phương trình hai ẩn
\(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\left( d \right)\\a'x + b'y = c'\,\,\,\left( {d'} \right)\end{array} \right.\).
Ta vẽ hai đường thẳng \((d)\) và \((d')\) trên cùng hệ trục tọa độ.
Nếu đường thẳng \((d)\) và \((d')\) trùng nhau thì hệ đã cho có vô số nghiệm
Lời giải chi tiết
\(\left( {III} \right)\left\{ \matrix{4x - 2y = - 6(d) \hfill \cr - 2x + y = 3(d')\hfill \cr} \right. \)
+) Xét đường thẳng (d):
Cho \(x = 0\) thì \( y = 3\) nên (d) đi qua điểm \((0;3)\)
Cho \(y = 0\) thì \( x =\dfrac{-3}{2}\) nên (d) đi qua điểm \((\dfrac{-3}{2};0)\)
+) Xét đường thẳng (d'):
Cho \(x = 0\) thì \( y = 3\) nên (d') đi qua điểm \((0;3)\)
Cho \(y = 0\) thì \( x =\dfrac{-3}{2}\) nên (d') đi qua điểm \((\dfrac{-3}{2};0)\)
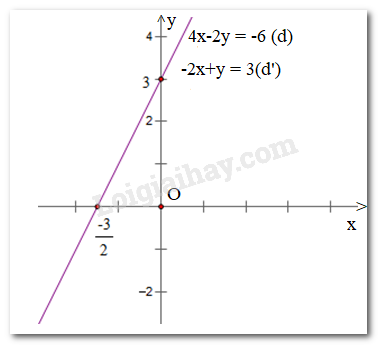
Hai đường thẳng trên trùng nhau nên hệ phương trình (III) có vô số nghiệm