Trả lời câu hỏi Bài 4 trang 108 SGK Toán 9 Tập 1 — Không quảng cáo

Đề bài

Hãy chứng minh khẳng định trên

Lời giải chi tiết

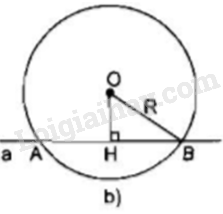
OH là một phần đường kính vuông góc với AB

Nên H là trung điểm của \(AB\) (định lý)

\( \Rightarrow HA{\rm{ }} = {\rm{ }}HB\)

Xét tam giác OHB vuông tại H có:

\(\eqalign{& O{B^2} = O{H^2} + H{B^2}  \cr &  \Rightarrow HB = \sqrt {O{B^2} - O{H^2}}  = \sqrt {{R^2} - O{H^2}}  \cr} \)

Vậy \(HA = HB = \sqrt {{R^2} - O{H^2}} \)