Trả lời câu hỏi Bài 4 trang 109 SGK Toán 9 Tập 1
Cho đường thẳng a và có một điểm O cách a là 3cm.
Đề bài
Cho đường thẳng a và có một điểm O cách a là 3cm. Vẽ đường tròn tâm O bán kính 5cm.
a) Đường thẳng a có vị trí như thế nào đối với đường tròn (O) ? Vì sao ?
b) Gọi B và C là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài BC.
Phương pháp giải - Xem chi tiết
a. Khoảng cách từ tâm O đến đường thẳng a nhỏ hơn độ dài bán kính thì a cắt đường tròn
b. Tính HC nhờ Định lí Pythago, rồi suy ra BC
Lời giải chi tiết
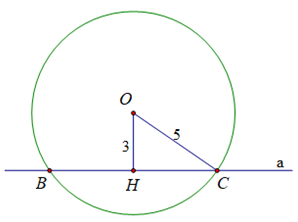
a) Đường thẳng a cắt đường tròn (O) tại 2 điểm phân biệt, vì khoảng cách d< R (3cm<5cm)
b) Kẻ \(OH\bot BC\) tại H.
Xét (O) có \(OH\) là 1 phần đường kính vuông góc với dây BC tại H nên H là trung điểm của BC (định lý)
Suy ra \(BC=2HC\)
Xét tam giác OHC vuông tại H, theo định lý Py-ta-go, ta có:
\(\eqalign{& HC = \sqrt {O{C^2} - O{H^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,\left( {cm} \right) \cr & \Rightarrow BC = 2HC = 8\left( {cm} \right) \cr} \)