Trắc nghiệm toán 6 bài tập cuối chương 1 cánh diều có đáp án — Không quảng cáo

Nhận thấy \(\left( {x + 15} \right)\) là thừa số chưa biết, \({5^3}\) là tích và \(5\) là thừa số đã biết.

Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

Từ đó tìm \(x\) bằng cách lấy tổng trừ số hạng đã biết.

\(\begin{array}{l}5(x + 15) = {5^3}\\5(x + 15) = 125\\\,\,\,\,x + 15\,\,\,\,= 125:5\\\,\,\,\,x + 15\,\,\,\, = 25\\\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 25 - 15\\\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= 10.\end{array}\)

Nhận thấy $65$ là số bị trừ;  ${4^{x + 2}}$  là số trừ và $1$ là hiệu nên muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.

Từ đó biến đổi về dạng hai lũy thừa cùng cơ số rồi cho hai số mũ bằng nhau.

\(\begin{array}{l}65 - {4^{x + 2}} = 1\\\,\,\,\,\,\,\,\,\,\,\,{4^{x + 2}}\,\, = 65 - 1\\\,\,\,\,\,\,\,\,\,\,{4^{x + 2}}\,\,\, = 64\\\,\,\,\,\,\,\,\,\,\,{4^{x + 2}}\,\,\, = {4^3}\\\,\,\,\,\,\,\;\;\,x + 2\,= 3\\\,\,\,\,\,\,\,\;\;x\,\,\,\,\,\,\,\,\,\,\,= 3 - 2\\\,\,\,\;\;\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\, = 1\end{array}\)

Chỉ ra các số tự nhiên thỏa mãn điều kiện là khác 0 và nhỏ hơn 5

Tập hợp các số tự nhiên khác 0 và nhỏ hơn 5 là tập hợp \(\left\{ {1;2;3;4} \right\}\)

Sử dụng công thức nhân hai lũy thừa cùng cơ số \({a^m}.{a^n} = {a^{m + n}}\,\,\,\left( {m;n \in N} \right)\) .

\({7^4}{.7^3} = {7^{4 + 3}} = {7^7}\) .

Dựa vào quy tắc chia hai lũy thừa cùng cơ số \({a^m}:{a^n} = {a^{m - n}}\,\,\,\left( {a \ne 0;m \ge n} \right)\)

Với \(x \ne 0\) thì \({x^8}:{x^2} = {x^{8 - 2}} = {x^6}\)

Dựa vào quy tắc nhân, chia hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\,\,\,\left( {m;n \in N} \right);\)\(\,\,{a^m}:{a^n} = {a^{m - n}}\,\,\,\left( {a \ne 0;m \ge n} \right)\)

Ta có:

\(\begin{array}{l}10000 = {10^4}\\{1020^0} = 1\\x.{x^7} = {x^{1 + 7}} = {x^8}\\{12^7}:{12^4} = {12^{7 - 4}} = {12^3}\end{array}\)

Do đó chỉ có đáp án D đúng.

Sử dụng công thức tính số số hạng của dãy số cách đều:

Số số hạng = ( số cuối – số đầu ) :  khoảng cách + 1

Số phần tử của tập hợp chính là số số hạng của dãy 3,6,9,…,150 và bằng:\(\left( {150 - 3} \right):3 + 1 = 50\)

Dựa vào phương pháp viết tập hợp bằng cách liệt kê các phần tử, chú ý đến yêu cầu của đề bài là \(5 < x < 50,x \,\vdots \, 15\).

Theo đề bài thì ta tìm trong khoảng từ 5 đến 50 các số chia hết cho 15 là: 15,30,45.

Do đó \(A = \left\{ {15,30,45} \right\}\) .

Dựa vào tính chất đặc trưng của các phần tử của tập hợp để viết tập hợp dưới dạng liệt kê

Từ đó chọn đáp án phù hợp

Trong cách viết \(A = \left\{ {x \in \mathbb{N}|2 < x \le 8} \right\}\), ta chỉ ra tính chất đặc trưng cho các phần tử x của tập hợp A đó là \(x > 2\) và \(x \le 8\) . Do đó 2 không là phần tử của tập A nên C sai.

Tập A còn có cách viết: \(A = \left\{ {3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8} \right\} \Rightarrow A\) có 6 phần tử nên đáp án B đúng. Dễ thấy A, D đều đúng.

Gọi B là tập hợp các số tự nhiên chẵn lớn hơn $1010$ nhưng không vượt quá $2012$. Ta viết B dưới dạng liệt kê phần tử. Nhận xét rằng dãy các phần tử của B là dãy cách đều 2 đơn vị Nên số phần tử của tập hợp cũng chính là số số hạng của dãy cách đều 2 đơn vị Số số hạng = (số hạng cuối - số hạng đầu) : khoảng cách + 1

Gọi B là tập hợp các số tự nhiên chẵn lớn hơn 1010 nhưng không vượt quá 2012. $B = \left\{ {1012;1014;1016;...;2008;2012} \right\}\;$ Xét dãy số $1012;{\rm{ }}1014;{\rm{ }}1016;{\rm{ }}...;{\rm{ }}2008;{\rm{ }}2012$ Ta thấy dãy trên là dãy số cách đều 2 đơn vị Số số hạng của dãy số trên là: $\left( {2012 - 1012} \right):2 + 1 = 501$ số hạng Số phần tử của tập hợp B cũng chính là số số hạng của dãy số trên Nên tập hợp các số tự nhiên chẵn lớn hơn $1010$ nhưng không vượt quá $2012$ có $501$ phần tử.

Tìm các phần tử thuộc tập hợp $M$ bằng cách lấy mỗi phần tử thuộc tập $X$ nhân lần lượt với từng phần tử thuộc tập $Y$.

$X = \left\{ {2;4} \right\};Y = \left\{ {1;3;7} \right\}\;$ Lấy mỗi phần tử thuộc tập hợp $X$ nhân lần lượt với từng phần tử thuộc tập hợp $Y$ ta được: \(2.1 = 2;2.3 = 6;2.7 = 14;4.1 = 4;4.3 = 12;4.7 = 28\) Vậy $M = \left\{ {2;6;14;4;12;28} \right\}\;$

Bước 1: Chuyển các lũy thừa cơ số $9$, cơ số $27$ về dạng lũy thừa cơ số $3$ bằng cách sử dụng công thức  \({\left( {{a^m}} \right)^n} = {a^{m.n}}\) , sử dụng định nghĩa để đưa $81$ về lũy thừa cơ số $3$. Bước 2: Thực hiện phép nhân các lũy thừa cùng cơ số ${a^m}.{a^n} = {a^{m + n}}$

Ta có ${9^3}{.27^2}.81\; = {\left( {3.3} \right)^3}.{\left( {3.3.3} \right)^2}.\left( {3.3.3.3} \right) = {\left( {{3^2}} \right)^3}.{\left( {{3^3}} \right)^2}{.3^4}$\( = {3^{2.3}}{.3^{3.2}}{.3^4} = {3^6}{.3^6}{.3^4} = {3^{6 + 6 + 4}} = {3^{16}}.\)

Thực hiện phép tính nâng lên lũy thừa rồi đến nhân chia cuối cùng là cộng trừ.

Ta có \({6^2}:4.3 + {2.5^2} = 36:4.3 + 2.25 = 9.3 + 50 = 27 + 50 = 77\) .

Bước 1: Phá ngoặc tròn rồi thực hiện phép tính trong ngoặc vuông Bước 2: Coi biểu thức trong ngoặc là số trừ chưa biết Muốn tìm số trừ chưa biết ta lấy số bị trừ trừ đi hiệu Bước 3: Coi \(2x\)  là số bị trừ chưa biết Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

Ta có:

$914 - [(x - 300) + x] = 654\;$

\(\begin{array}{l}914 - \left( {x - 300 + x} \right) = 654\\914 - \left( {2x - 300} \right) = 654\\2x - 300 = 914 - 654\\2x - 300 = 260\\2x = 260 + 300\\2x = 560\\x = 560:2\\x = 280\end{array}\) Vậy \(x = 280.\)

Áp dụng phương pháp tìm ƯCLN: phân tích các số ra thừa số nguyên tố, chọn các thừa số chung. Mỗi thừa số lấy số mũ nhỏ nhất, tích của các số đó là ƯCLN

$36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$

Ta số thừa số chung là $2;3$

Số mũ nhỏ nhất của $2$ là $2$; số mũ nhỏ nhất của $3$  là $1$

Vậy $ƯCLN\left( {36;60;72} \right) = {2^2}.3$.

Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.

Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Ta có:

$\begin{array}{l}9 = {3^2};24 = {2^3}.3\\ \Rightarrow BCNN\left( {9;24} \right) = {2^3}{.3^2} = 8.9 = 72\end{array}$

Bước 1: Phân tích 18; 32 và 50 ra thừa số nguyên tố Bước 2: Chọn ra thừa số nguyên tố chung và riêng của 18; 32 và 50 Bước 3: Lập tích các thừa số nguyên tố đã chọn mỗi thừa số lấy với số mũ lớn nhất của nó Tích đó chính là $BCNN\left( {18;32;50} \right)$

Ta có \(18 = {2.3^2};32 = {2^5};50 = {2.5^2}\)

Nên \(BCNN\left( {18;32;50} \right) = {2^5}{.3^2}{.5^2} = 7200.\)

Vì $7200$ chia hết cho $10$ nên $C$ đúng.

Bước 1: Xác định b bằng tính chất: “ Một số chia hết cho $2$ và $5$ thì có chữ số tận cùng bằng $0$” Bước 2: Thay b vào rồi tính tổng các chữ số của $\overline {2a4b} $ Để $\overline {2a4b} $ chia hết cho $3$ và $9$ thì tổng các chữ số phải chia hết cho $9$ Thử lần lượt các giá trị $a = 0,1,2,...,9$ vào xem giá trị nào thích hợp

Ta có: Để $\overline {2a4b} $ chia hết cho $2$ và $5$ thì $b = 0\;$ Thay $b = 0\;$ vào $\overline {2a4b} $ ta được $\overline {2a40} $ Tổng các chữ số là: \(2 + a + 4 + 0 = a + 6\) Thử lần lượt các giá trị $a = 0,1,2,...,9$ Ta thấy với \(a = 3\) thì  tổng các chữ số của $\overline {2a40}  = 2340$  là: \(6 + 3 = 9\, \vdots \,9\)

Nên \(2340\) chia hết cho $3$ và $9$.

Vậy với \(a = 3;b = 0\) thì \(\overline {2a4b} \) chia hết cho \(2;3;5\) và \(9.\)

Ta đưa về bài toán tìm $ƯCLN$ của $525; 875; 280.$ Bước 1: Phân tích $525; 875; 280$ ra thừa số nguyên tố. Bước 2: Chọn ra các thừa số nguyên tố chung. Bước 3: Lập tích các thừa số nguyên tố chung đó, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Đó chính là số cần tìm.

Vì $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$ và $a$ là số lớn nhất$ \Rightarrow a = ƯCLN\left( {525;{\rm{ }}875;{\rm{ }}280} \right)$ Ta có:

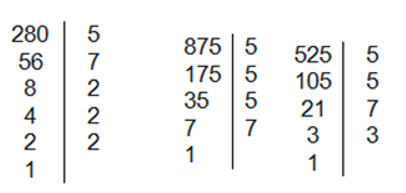
Nên \(525 = {3.5^2}.7;875 = {5^3}.7;280 = {2^3}.5.7\) $ \Rightarrow \;a = $ ƯCLN$\left( {525;875;280} \right) = 5.7 = 35\;$

Sử dụng quy tắc nhân, chia hai lũy thừa cùng cơ số và thứ tự thực hiện phép tính để tính giá trị của biểu thức.

Ta có

$\begin{array}{l}A = \left( {6888:56-{{11}^2}} \right).152 + 13.72 + 13.28\\\,\,\,\,\,\, = \left( {6888:56 - 121} \right).152 + 13.72 + 13.28\\\,\,\,\,\,\, = \left( {123 - 121} \right).152 + 13.72 + 13.28\\\,\,\,\,\,\, = 2.152 + 13.\left( {72 + 28} \right)\\\,\,\,\,\,\, = 2.152 + 13.100\\\,\,\,\,\,\, = 304 + 1300\\\,\,\,\,\,\, = 1604\end{array}$

$\begin{array}{l}B = \left[ {5082:\left( {{{17}^{29}}:{{17}^{27}}-{{16}^2}} \right) + 13.12} \right]:31 + {9^2}\\\,\,\,\,\, = \left[ {5082:\left( {{{17}^{29 - 27}}-{{16}^2}} \right) + 13.12} \right]:31 + {9^2}\\\,\,\,\,\, = \left[ {5082:\left( {{{17}^2}-{{16}^2}} \right) + 13.12} \right]:31 + {9^2}\\\,\,\,\,\, = \left[ {5082:\left( {289 - 256} \right) + 13.12} \right]:31 + {9^2}\\\,\,\,\,\, = \left( {5082:33 + 13.12} \right):31 + {9^2}\\\,\,\,\,\, = \left( {154 + 156} \right):31 + {9^2}\\\,\,\,\,\, = 310:31 + 81\\\,\,\,\,\, = 10 + 81 = 91.\end{array}$

Suy ra \(A - 2B = 1422.\)

+ Tìm bội chung của \(5\) và \(6\)

+ Kết hợp với điều kiện \(0 < x < 100\) để tìm các số thỏa mãn.

Do \(x \vdots 5;x \vdots 6 \Rightarrow x \in BC\left( {5;6} \right) = \left\{ {0;30;60;90;120;...} \right\}\)

Mà \(0 < x < 100\) nên \(x \in \left\{ {30;60;90} \right\}\).

Vậy \(x \in \left\{ {30;60;90} \right\}\).

Áp dụng kiến thức về dấu hiệu chia hết:

Dấu hiệu chia hết cho $9$ là tổng tất cả các chữ số chia hết cho $9$

Dấu hiệu chia hết của $1$  tổng: nếu $a \vdots c;b \vdots c \Rightarrow (a + b) \vdots c$

Ta có $A = 18 + 36 + 72 + 2x$ mà $A \vdots 9;18 \vdots 9;36 \vdots 9;72 \vdots 9 \Rightarrow 2x \vdots 9 \Rightarrow x \vdots 9$

Mà $45 < x < 55 \Rightarrow x = 54$

Vậy $x = 54$.

Áp dụng kiến thức về bội chung, nếu $a \vdots b;a \vdots c;a \vdots d$ thì $a$ là bội chung của $b,c,d$.

Từ đề bài suy ra số học sinh khối 6 là bội của 10;12;15.

Kết hợp điều kiện số học sinh trong khoảng từ 100 đến 150 để tìm số thích hợp

Gọi số học sinh khối 6 là \(x\left( {x \in {N^*}} \right)\) (học sinh)

Theo bài ra ta có:

\(x \vdots 10,x \vdots 12;x \vdots 15 \Rightarrow x \in BC\left( {10;12;15} \right)\) và \(100 \le x \le 150\).

Ta có

$\begin{array}{l}10 = 2.5;12 = {2^2}.3;15 = 3.5\\ \Rightarrow BCNN(10;12;15) = {2^2}.3.5 = 60\\ \Rightarrow BC\left( {10;12;15} \right) = \left\{ {0;60;120;180;...} \right\}\\ \Rightarrow x \in  \left\{ {0;60;120;180;...} \right\} \end{array}$

Mà \(100 \le x \le 150\) nên \(x = 120\).

Vậy số học sinh khổi 6 là $120$ bạn.

Sử dụng các quy tắc để biến đổi hai lũy thừa hoặc cùng cơ số hoặc cùng số mũ và sử dụng quy tắc:

+) Nếu \(n < m\) thì \({a^n} < {a^m}\left( {a > 1;m,n \in N} \right)\)

+) Nếu \(a < b\) thì \({a^n} < {b^n}\left( {a,b \in \mathbb{N};n \in \mathbb{N}^*} \right)\)

Ta có:

\(\)\(\)\(\begin{array}{l}{202^{303}} = {202^{3.101}} = {\left( {{{202}^3}} \right)^{101}}\\{303^{202}} = {303^{2.101}} = {\left( {{{303}^2}} \right)^{101}}\end{array}\)

Ta so sánh \({202^3}\) và \({303^2}\)

\(\begin{array}{l}{202^3} = {\left( {2.101} \right)^3} = {2^3}{.101^3} = {2^3}{.101^{1 + 2}} = {2^3}{.101.101^2} = {8.101.101^2} = {808.101^2}\\{303^2} = {\left( {3.101} \right)^2} = {3^2}{.101^2} = {9.101^2}\end{array}\)

Vì \(9 < 808\) nên \({9.101^2} < {808.101^2}\) hay \({303^2} < {202^3}\)

Do đó \({\left( {{{303}^2}} \right)^{101}} < {\left( {{{202}^3}} \right)^{101}}\)

Vậy \({303^{202}} < {202^{303}}\) .

Bước 1: Nếu gọi số đĩa là x cái, lập luận để có $x = $ƯCLN$\left( {840;2352;560} \right)$ Bước 2: Phân tích các số $840;{\rm{ }}2352;{\rm{ }}560$ ra thừa số nguyên tố Bước 3: Lập tích các thừa số nguyên tố chung, mỗi thừa số lấy với số mũ nhỏ nhất Đó chính là số đĩa cần tìm

Gọi số đĩa cần chẩn bị là x cái \(\left( {x \in {N^*}} \right)\) Vì số bánh, kẹo và quýt được chia đều vào các đĩa nên: $840\;\, \vdots x{\rm{ }};{\rm{ }}2352\,\; \vdots \;x{\rm{ }};{\rm{ }}560\;\, \vdots \;x$ Và $x$ là lớn nhất nên $x = $ƯCLN$\left( {840;2352;560} \right)$ Ta có: \(840 = {2^3}.3.5.7;560 = {2^4}.5.7;2352 = {2^4}{.3.7^2}\)

Suy ra  ƯCLN$\left( {840;{\rm{ }}2352;{\rm{ }}560} \right){\rm{ }} = \;{2^3}.7\; = 56$ Vậy số đĩa nhiều nhất cần chuẩn bị là $56$ .

Sử dụng công thức nhân hai lũy thừa cùng cơ số, tính chất phân phối của phép nhân với phép cộng để đưa về so sánh hai lũy thừa cùng cơ số, từ đó tìm ra x.

\(\begin{array}{l}{5^x} + {5^{x + 2}} = 650\\{5^x} + {5^x}{.5^2} = 650\\{5^x} + {5^x}.25 = 650\\{5^x}.\left( {1 + 25} \right) = 650\\{5^x}.26 = 650\\{5^x} = 650:26\\{5^x} = 25\\{5^x} = {5^2}\\x = 2\end{array}\)

Sử dụng tính chất giao hoán, tính chất kết hợp, tính chất phân phối của phép nhân với phép cộng để tính một cách hợp lý.

Ta có:

\(\begin{array}{l}28.231 + 69.28 + 72.231 + 69.72\\ = \left( {28.231 + 69.28} \right) + \left( {72.231 + 69.72} \right)\\ = 28.\left( {231 + 69} \right) + 72.\left( {231 + 69} \right)\\ = 28.300 + 72.300\\ = 300.\left( {28 + 72} \right)\\ = 300.100\\ = 30000\end{array}\)

Nhận thấy số 30000 gần với số 30005  nhất trong các đáp án  nên chọn A.

Thu gọn vế phải.

Sử dụng quy tắc nhân, chia hai lũy thừa cùng cơ số và quy tắc thứ tự thực hiện phép tính để tìm x.

$\begin{array}{l}\,\,\,\,\,\,\;\left( {2x-130} \right):4 + 213 = {5^2} + 193\\\,\,\,\,\,\,\left( {2x-130} \right):4 + 213 = 25 + 193\\\,\,\,\,\,\,\left( {2x-130} \right):4 + 213 = 218\\\,\,\,\,\,\,\left( {2x-130} \right):4= 218 - 213\\\,\,\,\,\,\,\left( {2x-130} \right):4= 5\\\,\,\,\,\,\,\,2x-130= 5.4\\\,\,\,\,\,\,\,2x-130= 20\\\,\,\,\,\,\,\,2x= 20 + 130\\\,\,\,\,\,\,2x= 150\\\,\,\,\,\,\,\,\,\,x= 150:2\\\,\,\,\,\,\,\,\,x= 75\end{array}$

Sử dụng quy tắc nhân, chia hai lũy thừa cùng cơ số và thứ tự thực hiện phép tính đưa về việc so sánh hai lũy thừa cùng cơ số để tìm $x$.

Ta có

\(\begin{array}{l} + )\,{x^3} - {2^3} = {2^5} - \left( {{3^{16}}:{3^{14}} + {2^8}:{2^6}} \right)\\{x^3} - {2^3} = {2^5} - \left( {{3^{16 - 14}} + {2^{8 - 6}}} \right)\\{x^3} - {2^3} = {2^5} - \left( {{3^2} + {2^2}} \right)\\{x^3} - {2^3} = {2^5} - \left( {9 + 4} \right)\\{x^3} - 8 = 32 - 13\\{x^3} - 8 = 19\\{x^3} = 19 + 8\\{x^3} = 27\\{x^3} = {3^3}\\x = 3\end{array}\)

Suy ra \({x_1} = 3.\)

\(\begin{array}{l}{\rm{ + )}}\,2448:\left[ {158 - 7.{{\left( {x - 6} \right)}^3}} \right] = 24\\158 - 7.{\left( {x - 6} \right)^3} = 2448:24\\158 - 7.{\left( {x - 6} \right)^3} = 102\\7.{\left( {x - 6} \right)^3} = 158 - 102\\7.{\left( {x - 6} \right)^3} = 56\\{\left( {x - 6} \right)^3} = 56:7\\{\left( {x - 6} \right)^3} = 8 = {2^3}\\x - 6 = 2\\x = 2 + 6\\x = 8\end{array}\)

Suy ra \({x_2} = 8\)

Từ đó ta có \({x_1} = 3;{x_2} = 8 \Rightarrow {x_1}.{x_2} = 24.\)

Sử dụng phương pháp tách cấu tạo số theo các chữ số trong hệ thập phân để tìm ra mối quan hệ của các chữ số, ta xác định được cụ thể từng chữ số.

\(\overline {ab} = a.10 + b\,\left( {0 < a \le 9;0 \le b \le 9;a,b \in N} \right)\)

Gọi số có hai chữ số cần tìm là \(\overline {ab} \left( {0 < a \le 9;0 \le b \le 9};\, a,b \in N \right)\).

Khi viết thêm chữ số $0$ vào giữa hai chữ số ta được số mới là \(\overline {a0b} \) .

Theo bài ra ta có:

\(\begin{array}{l}\overline {a0b}  = 7.\overline {ab} \\100.a + b = 7.\left( {10.a + b} \right)\\100.a + b = 70.a + 7.b\\100.a - 70.a = 7.b - b\\30.a = 6.b\\5.a = b\end{array}\)

Vì $a,b$ là các chữ số và \(a \ne 0\) nên \(a = 1;b = 5\) .

Vậy số cần tìm là $15$.

Dựa vào thứ tự trong tập hợp số tự nhiên để viết dạng tổng quát của 4 số tự nhiên liên tiếp, sau đó lập tổng của chúng để tìm ra 4 số đó..

Gọi \(n \in \mathbb{N}\)  ta có các số: n; n+1; n+2; n+3 là 4 số tự nhiên liên tiếp.

Theo đề bài ta có:

\(\begin{array}{l}n + \left( {n + 1} \right) + \left( {n + 2} \right) + \left( {n + 3} \right) = 2010\\4.n + 6 = 2010\\4n= 2010 - 6\\4n= 2004\\n = 2004:4\\n = 501.\end{array}\)

Vậy 4 số tự nhiên đó là 501; 502; 503; 504.

Số nhỏ nhất là 501.

Chia số trang thành các nhóm để dễ dàng tính được số chữ số cần dùng trong mỗi nhóm, từ đó tính được tổng số chữ số cần dùng.

Ta chia các số trang của cuốn sách thành 4 nhóm:

+ Nhóm các số có $1$ chữ số (từ trang $1$ đến trang $9$): số chữ số cần dùng là $9$.

+ Nhóm các số có hai chữ số (từ trang $10$ đến trang $99$): số trang sách là: \(\left( {99 - 10} \right):1 + 1 = 90\), số chữ số cần dùng là: \(90.2 = 180\) .

+ Nhóm các số có $3$ chữ số (từ trang $100$ đến trang $999$): số trang sách là: \(\left( {999 - 100} \right):1 + 1 = 900\), số chữ số cần dùng để đánh số trang nhóm này là: \(900.3 = 2700\).

+Nhóm các số có $4$ chữ số (từ trang $1000$ đến trang $1031$): số trang sách là: \(\left( {1031 - 1000} \right):1 + 1 = 32\) ; số chữ số cần dùng là \(32.4 = 128\) .

Vậy tổng số chữ số cần dùng để đánh số trang cuốn sách đó là: \(9 + 180 + 2700 + 128 = 3017\)

Nhân thêm vào hai vế của biểu thức $P$ với \({5^3}\) để được biểu thức mới, sau đó lấy biểu thức mới trừ đi biểu thức ban đầu, biến đổi để được biểu thức rút gọn của $P$.

\(\begin{array}{l}P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\\{5^3}.P = {5^3}.\left( {1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}} \right) = {5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}\\125.P = {5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}\\ \Rightarrow 125.P - P = \left( {{5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}} \right) - \left( {1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}} \right)\\ \Rightarrow 124.P = {5^{102}} - 1\end{array}\)

Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.

Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$

Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:

\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)

\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)

\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)

\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)

Suy ra \(1 \vdots d\)

\(d = 1\)

Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.