Trắc nghiệm Bài 11: Phân tích một số ra thừa số nguyên tố Toán 6 Cánh diều
Đề bài
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
-
A.
Các số \({p_1};\,{p_2};...;\,{p_k}\) là các số dương.
-
B.
Các số \({p_1};\,{p_2};...;\,{p_k} \in P\)(với $P$ là tập hợp các số nguyên tố).
-
C.
Các số \({p_1};\,{p_2};...;\,{p_k} \in N\).
-
D.
Các số \({p_1};\,{p_2};...;\,{p_k}\) tùy ý.
Phân tích số $18$ thành thừa số nguyên tố:
-
A.
$18 = 18.1$
-
B.
$18 = 10 + 8$
-
C.
$18 = {2.3^2}$
-
D.
$18 = 6 + 6 + 6$
Cho số $a = {2^2}.7$, hãy viết tập hợp tất cả các ước của $a$:
-
A.
Ư\(\left( a \right)\)${\rm{ = \{ 4;7\} }}$
-
B.
Ư$\left( a \right)$ ${\rm{ = \{ 1;4;7\} }}$
-
C.
Ư$\left( a \right)$${\rm{ = \{ 1;2;4;7;28\} }}$
-
D.
Ư$\left( a \right)$${\rm{ = \{ 1;2;4;7;14;28\} }}$
Cho ${a^2}.b.7 = 140$ với \(a,b\) là các số nguyên tố, vậy \(a\) có giá trị là bao nhiêu:
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Cho số ${\rm{150 = 2}}{\rm{.3}}{\rm{.}}{{\rm{5}}^2}$, số lượng ước của $150$ là bao nhiêu:
-
A.
$6$
-
B.
$7$
-
C.
$8$
-
D.
$12$
-
A.
$2,4,6$
-
B.
$2,6,4$
-
C.
$6,4,2$
-
D.
$6,2,4$
Số nào trong các số sau là ước nguyên tố của 52?
-
A.
26
-
B.
3
-
C.
13
-
D.
1
Khi phân tích 104 thành tích các thừa số nguyên tố thì số mũ của thừa số 2 là
-
A.
2
-
B.
1
-
C.
3
-
D.
4
Lời giải và đáp án
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
-
A.
Các số \({p_1};\,{p_2};...;\,{p_k}\) là các số dương.
-
B.
Các số \({p_1};\,{p_2};...;\,{p_k} \in P\)(với $P$ là tập hợp các số nguyên tố).
-
C.
Các số \({p_1};\,{p_2};...;\,{p_k} \in N\).
-
D.
Các số \({p_1};\,{p_2};...;\,{p_k}\) tùy ý.
Đáp án : B
- Áp dụng kiến thức về phân tích $1$ số thành thừa số nguyên tố (các thừa số trong tích phải là số nguyên tố)
Khi phân tích một số \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\) ra thừa số nguyên tố thì các số \({p_1},{p_2},...,{p_k}\) phải là các số nguyên tố.
Phân tích số $18$ thành thừa số nguyên tố:
-
A.
$18 = 18.1$
-
B.
$18 = 10 + 8$
-
C.
$18 = {2.3^2}$
-
D.
$18 = 6 + 6 + 6$
Đáp án : C
- Phân tích số ra thành số nguyên tố.
- Đáp án A sai vì 1 không phải là số nguyên tố
- Đáp án B sai vì đây là phép cộng.
- Đáp án C đúng vì $2$ và $3$ là $2$ số nguyên tố và ${2.3^2} = 2.9 = 18$
- Đáp án D sai vì đây là phép cộng.
Cho số $a = {2^2}.7$, hãy viết tập hợp tất cả các ước của $a$:
-
A.
Ư\(\left( a \right)\)${\rm{ = \{ 4;7\} }}$
-
B.
Ư$\left( a \right)$ ${\rm{ = \{ 1;4;7\} }}$
-
C.
Ư$\left( a \right)$${\rm{ = \{ 1;2;4;7;28\} }}$
-
D.
Ư$\left( a \right)$${\rm{ = \{ 1;2;4;7;14;28\} }}$
Đáp án : D
- Thực hiện phép tính để tìm ra $a$.
- Áp dụng kiến thức ước của $1$ số.
- Liệt kê tất cả các ước của số đó.
Ta có $a = {2^2}.7 = 4.7 = 28$
$28 = 28.1 = 14.2 = 7.4 = 7.2.2$, vậy ${\rm{U}}\left( {28} \right){\rm{ = }}\left\{ {{\rm{1;2;4;7;14;28}}} \right\}$
Cho ${a^2}.b.7 = 140$ với \(a,b\) là các số nguyên tố, vậy \(a\) có giá trị là bao nhiêu:
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : B
- Phân tích số \(140\) thành tích các thừa số nguyên tố.

Suy ra $140 = {2^2}.5.7 = {a^2}.b.7$ nên \(a = 2\).
Cho số ${\rm{150 = 2}}{\rm{.3}}{\rm{.}}{{\rm{5}}^2}$, số lượng ước của $150$ là bao nhiêu:
-
A.
$6$
-
B.
$7$
-
C.
$8$
-
D.
$12$
Đáp án : D
- Áp dụng kiến thức: Nếu $m = {a^x}.{b^y}.{c^z}$ với \(a,b,c\) là các số nguyên tố thì $m$ có $\left( {x + 1} \right)\left( {y + 1} \right)\left( {z + 1} \right)$ ước.
Ta có ${\rm{150 = 2}}{\rm{.3}}{\rm{.}}{{\rm{5}}^2}$, vậy $x = 1;y = 1;z = 2$
Vậy số lượng ước của số $150$ là $\left( {1 + 1} \right)\left( {1 + 1} \right)\left( {2 + 1} \right) = 2.2.3 = 12$
-
A.
$2,4,6$
-
B.
$2,6,4$
-
C.
$6,4,2$
-
D.
$6,2,4$
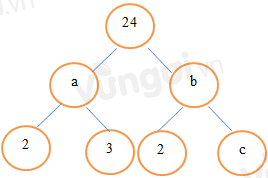
Đáp án : C
$a=2.3=6$
$6.b=24=>b=4$
$2.c=b=>c=4:2=2$
Vậy $a=6,b=4,c=2$.
Số nào trong các số sau là ước nguyên tố của 52?
-
A.
26
-
B.
3
-
C.
13
-
D.
1
Đáp án : C
Xét từng đáp án.
Loại các đáp án không là số nguyên tố hoặc không là ước của 52.
Ta thấy 26 và 1 đều là các ước của 52 nhưng không là số nguyên tố.
số 3 là số nguyên tố nhưng không là ước của 52 nên loại A.
13 là một ước của 52 và 13 là một số nguyên tố nên 13 là ước nguyên tố của 52.
Khi phân tích 104 thành tích các thừa số nguyên tố thì số mũ của thừa số 2 là
-
A.
2
-
B.
1
-
C.
3
-
D.
4
Đáp án : C
$104=2.2.2.13=2^3.13$
Vậy số mũ của thừa số 2 là 3.