Trắc nghiệm Vật Lí 10 bài 8 Chân trời sáng tạo có đáp án — Không quảng cáo

• A.

  \(2,25m\)

• B.

  \(0,75m\)

• C.

  \(1,25m\)

• D.

  \(0,5m\)

• A.

  4s

• B.

  3s

• C.

  5s

• D.

  9s

• A.

  \(43m\)

• B.

  \(40m\)

• C.

  \(15m\)

• D.

  \(30m\)

• A.

  \(4,5m\)

• B.

  \(10m\)

• C.

  \(15m\)

• D.

  \(20m\)

A, C, D - đúng

B - sai vì: Trong chân không, mọi vật đều rơi nhanh như nhau.

Ở một nơi trên trái đất  (tức ở một vĩ độ xác định) => cùng g

=> Thời gian rơi tự do của một vật phụ thuộc vào độ cao của vật

A, C, D - đúng

B - sai vì ở những nơi khác nhau - gia tốc rơi tự do sẽ khác nhau.

A - sai vật nào có lực cản nhỏ hơn sẽ rơi nhanh hơn

B - sai vì trong chân không, các vật rơi như nhau

C - đúng

D - sai vì ở cùng một nơi trên Trái Đất, các vật đều rơi tự do với cùng một gia tốc

Sử dụng phương trình chuyển động của vật rơi tự do: \(y = {y_0} + {v_0}t + \frac{1}{2}g{t^2}\)

+ Xác định vận tốc ban đầu \({v_0}\)

+ Xác định vị trí ban đầu của vật so với gốc tọa độ

Ta có:

+ Vật rơi không vận tốc đầu: \( \to {v_0} = 0\)

Gốc tọa độ tại O ở phía dưới A một đoạn 196m, chiều dương hướng xuống

+ Tọa độ ban đầu của vật: \({y_0} =  - 196m\)

=> Phương trình chuyển động của vật:  \(y =  - 196 + \frac{1}{2}.9,8{t^2} = 4,9{t^2} - 196\left( m \right)\)

A - sai vì: Khi không có lực cản các vật đều rơi như nhau

B - đúng

C - sai vì: Các vật rơi với cùng gia tốc \(g\) như nhau tại cùng 1 nơi

D - sai vì: Vận tốc của vật chạm đất phụ thuộc vào độ cao của vật khi rơi

Vận dụng định nghĩa về sự rơi tự do

Sự rơi tự do (chuyển động rơi tự do) là sự rơi của các vật chỉ chịu tác dụng của trọng lực.

Ta có: Sự rơi tự do (chuyển động rơi tự do) là sự rơi của các vật chỉ chịu tác dụng của trọng lực.

=> Chuyển động của một viên gạch rơi từ độ cao 3m xuống đất là chuyển động rơi tự do.

Khi loại bỏ được ảnh hưởng của không khí thì các vật sẽ rơi tự do hay nói cách khác là chuyển động thẳng nhanh dần đều

• A.

  \(2,25m\)

• B.

  \(0,75m\)

• C.

  \(1,25m\)

• D.

  \(0,5m\)

• A.

  4s

• B.

  3s

• C.

  5s

• D.

  9s

+ Chọn hệ quy chiếu: gốc tọa độ, chiều chuyển động

+ Chọn gốc thời gian

+ Viết phương trình chuyển động của 2 giọt nước

+ Giải phương trình : \({s_1} - {s_2} = \Delta s\)

+ Chọn HQC :

- Gốc tọa độ O tại vị trí rơi.

- Chiều dương hướng xuống

+ Gốc thời gian

\(t = 0\) là lúc giọt \(2\) rơi \( \to \left\{ \begin{array}{l}{t_{{0_1}}} \ne 0\\{t_{{0_2}}} = 0\end{array} \right.\)

+ Phương trình chuyển động của \(2\) giọt nước là :

\({s_1} = \frac{1}{2}g{\left( {t + {t_{01}}} \right)^2}\) và

\({s_2} = \frac{1}{2}g{t^2}\)

+ Theo đề bài tại

\(t = 2s\) ta có : \({s_1} - {s_2} = 25m\)

\(\begin{array}{l} \leftrightarrow \frac{1}{2}g{\left( {t + {t_{01}}} \right)^2} - \frac{1}{2}g{t^2} = 25\\ \leftrightarrow 5{\left( {2 + {t_{01}}} \right)^2} - {5.2^2} = 25\\ \leftrightarrow t_{01}^2 + 4{t_{01}} - 5 = 0\\ \to \left[ \begin{array}{l}{t_{01}} = 1\\{t_{01}} =  - 5(loai)\end{array} \right.\end{array}\)

\( \to {t_{01}} = 1s\)

Vậy giọt thứ 2 rơi sau giọt thứ nhất 1s.

+ Chọn hệ quy chiếu: Vị trí ban đầu, chiều dương

+ Chọn gốc thời gian

+ Viết phương trình chuyển động của mỗi vật: \(s = \frac{1}{2}g{t^2}\)

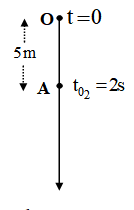
+ Chọn HQC :

- O tại vị trí thả vật, chiều dương hướng xuống

+ Gốc thời gian \(t = 0\): lúc thả vật 1 \( \to \left\{ \begin{array}{l}{t_{{0_1}}} = 0\\{t_{{0_2}}} = 1s\end{array} \right.\)

+ Lập các phương trình chuyển động :

- PT của vật 1:

\({s_1} = \frac{1}{2}g{t^2} = 5{t^2}\) (1)

- PT của vật 2:

\({s_2} = {v_0}\left( {t - 1} \right) + \frac{1}{2}g{\left( {t - 1} \right)^2} = {v_0}\left( {t - 1} \right) + 5{\left( {t - 1} \right)^2}\)  (2)

Ta có:

+ Thời gian vật 1 chuyển chạm đất là: \({s_1} = 5{t^2} = 45 \to t = \sqrt {\frac{{45}}{5}}  = 3{\rm{s}}\)

+ Mặt khác, vật 1 và vật 2 chạm đất cùng lúc, thay \(t = 3{\rm{s}}\) vào phương trình (2), ta được:

\(\begin{array}{l}{v_0}\left( {3 - 1} \right) + 5{\left( {3 - 1} \right)^2} = 45\\ \leftrightarrow 2{v_0} + 20 = 45\\ \to {v_0} = 12,5m/s\end{array}\)

+ Viết phương trình chuyển động của mỗi vật

- Khi bị ném

- Khi rơi tự do

+ Vận dụng biểu thức: \({\rm{s}} = {v_0}t + \frac{1}{2}g{t^2}\)

Các phương trình chuyển động:

+ PT chuyển động rơi tự do: \({s_1} = \frac{1}{2}g{t^2} = 5{t^2}\) (1)

+ PT chuyển động khi vật bị ném: \({s_2} = {v_0}t' + \frac{1}{2}gt{'^2} = {v_0}t + 5t{'^2}\)  (2)

Ta có, thời gian vật rơi tự do chạm đất:\({s_1} = 5{t^2} = 20 \to t = 2{\rm{s}}\)

Theo đề : \(t - t' = 1 \to t' = 1{\rm{s}}\)

Thay vào (2) ta được : \(20 = 5 + {v_0} \to {v_0} = 15m/s\)

+ Vận dụng phương trình chuyển động của vật rơi tự do: \(s = \dfrac{1}{2}g{t^2}\)

+ Vận dụng phương trình vận tốc của vật rơi tự do: \(v = gt\)

+ Phương trình của chuyển động rơi tự do: \(s = \dfrac{{g{t^2}}}{2} = 9,8.\dfrac{{{t^2}}}{2} = 4,9{t^2}\)

+ Phương trình vận tốc của vật: \(v = {v_o} + gt = 9,8t\)

+ Khi vật chạm đất: \(s = 9,8.\dfrac{{{t^2}}}{2} = 19,6 \Rightarrow t = 2\left( s \right)\)

Vận tốc của vật khi chạm đất là: \(v = gt = 9,8t = 9,8.2 = 19,6m/s\)

• A.

  \(43m\)

• B.

  \(40m\)

• C.

  \(15m\)

• D.

  \(30m\)

• A.

  \(4,5m\)

• B.

  \(10m\)

• C.

  \(15m\)

• D.

  \(20m\)

Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\)

+ Trong \(2\left( s \right)\) cuối cùng quãng đường vật đi được là \(180{\rm{ }}m\) ta có:

\(\begin{array}{l}\Delta S = {S_t} - {S_{t - 2}} \\= 180 = \dfrac{{g{t^2}}}{2} - \dfrac{{g.{{\left( {t - 2} \right)}^2}}}{2} \\\Rightarrow {t^2} - {\left( {t - 2} \right)^2} = 36\\ \Rightarrow 4t -4 = 36 \Rightarrow t = 10\left( s \right)\end{array}\)

+ Độ cao buông vật là: \(s = \dfrac{{g{t^2}}}{2}\) $= 500 m$

+ Vận dụng phương trình chuyển động của vật rơi tự do : \(S = \frac{1}{2}g{t^2}\)

+ Quãng đường vật đi được trong giây thứ n : \(\Delta S = {S_n} - {S_{n - 1}}\)

+ Phương trình chuyển động của vật rơi tự do là : \(S = \frac{{g{t^2}}}{2}\)

+ Quãng đường vật đi được trong giây thứ 3 là: \(\Delta S = {S_3} - {S_2} = \frac{{{{10.3}^2}}}{2} - \frac{{{{10.2}^2}}}{2} = 25m\)

+ Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\)

+ Tính thời gian vật rơi hết quãng đường : \(t = \sqrt {\dfrac{{2{\rm{s}}}}{g}} \)

Phương trình chuyển động của vật rơi tự do là: \(s = \dfrac{{g{t^2}}}{2}\)

+ Thời gian vật đi hết quãng đường \(74,8m\) là:

\(s = \dfrac{{g{t^2}}}{2} \Rightarrow 74,8 = 9,8.\dfrac{{{t^2}}}{2} \\\Rightarrow t = 3,91\left( s \right)\)

+ Thời gian để vật đi hết 20m đầu là:

\(s = \dfrac{{g{t^2}}}{2} = 20 \Rightarrow {t^2} = \dfrac{{20.2}}{{9,8}} \\\Rightarrow t = 2,02\left( s \right)\)

+ Công thức tính quãng đường vật đi trong \(20m\) cuối là: \(74,8 - \dfrac{{{gt^2}}}{2} = 20 \\\Rightarrow \dfrac{{g{t^2}}}{2} = 54,8 \\\Rightarrow t = 3,34\left( s \right)\)

Thời gian để vật đi hết \(20m\) cuối là \(3,91{\rm{ }}-{\rm{ }}3,34{\rm{ }} = {\rm{ }}0,57{\rm{ }}\left( s \right)\)

Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \dfrac{1}{2}g{t^2}\)

+ Sau \(2{\rm{ }}\left( s \right)\) viên bi B đi được quãng đường là: \({s_{{B_{}}}} = g\dfrac{{{t^2}}}{2} = 10.\dfrac{{{2^2}}}{2} = 20\left( m \right)\)

Vì viên bi A rơi sau viên bi B \(0,5s\) nên quãng đường viên bi A đi được sau \(2s\) là:

\({s_{{A_{}}}} = g\dfrac{{{t^2}}}{2} = 10.\dfrac{{1,{5^2}}}{2} = 11,25\left( m \right)\)

+ Sau \(2s\) khoảng cách giữa hai viên bi là: \(\Delta s = {s_B} - {s_A} = 20 - 11,25 = 8,75\left( m \right)\)

Vận dụng phương trình chuyển động của vật rơi tự do : \(s = \frac{1}{2}g{t^2}\)

Giả sử giọt thứ nhất rơi trước giọt thứ 2, khi đó ta có sau khi giọt thứ 2 rơi được 1s thì giọt thứ nhất rơi được 2s

Vậy khoảng cách giữa chúng khi giọt thứ 2 rơi được 1s là: \(\Delta s = {s_1} - {s_2} = \frac{{g{t_1}^2}}{2} - \frac{{g.{t_2}^2}}{2} = 10.\frac{{{2^2}}}{2} - 10.\frac{{{1^2}}}{2} = 15\left( m \right)\)

Quãng đường vật rơi trong  n giây : \({s_{t = n}} = \dfrac{1}{2}g.{n^2}\)

Quãng đường vật rơi trong giây thứ n:

\({s_n} = {s_{t = n}} - {s_{t = n - 1}} = \dfrac{1}{2}g.{n^2} - \dfrac{1}{2}g.{\left( {n - 1} \right)^2}\)

Ta có : \(\left\{ \begin{array}{l}h = 80m\\g = 10m/{s^2}\end{array} \right.\)

Quãng đường vật rơi trong 2s là :

\({s_{t = 2}} = \dfrac{1}{2}g.{t^2} = \dfrac{1}{2}{.10.2^2} = 20m\)

Quãng đường vật rơi trong giây thứ hai là:

\({s_2} = {s_{t = 2}} - {s_{t = 1}} = \dfrac{1}{2}{.10.2^2} - \dfrac{1}{2}{.10.1^2} = 15m\)

Áp dụng công thức tính quãng đường đi được của vật rơi tự do trong thời gian t giây:

\(s = \frac{1}{2}.g.{t^2}\)

Trong giây cuối cùng quãng đường vật đi được là

\({S_c} = h - \frac{1}{2}.g.{({t_h} - 1)^2}\)

với t _h là thời gian vật rơi chạm đất:

\({t_h} = \sqrt {\frac{{2h}}{g}} \)

Quãng đường đi được của vật rơi tự do trong thời gian \(\sqrt{3}s\)đầu tiên

\(s=\frac{1}{2}.g.{{t}^{2}}=\frac{1}{2}.g.3=1,5g\)

Trong giây cuối cùng quãng đường vật đi được là

\({{S}_{c}}=h-\frac{1}{2}.g.{{({{t}_{h}}-1)}^{2}}\)

với \({{t}_{h}}\) là thời gian vật rơi chạm đất:  \({{t}_{h}}=\sqrt{\frac{2h}{g}}\text{ }\)

Vậy ta có: \({{S}_{c}}=h-\frac{1}{2}.g.{{\left( \sqrt{\frac{2h}{g}}-1 \right)}^{2}}=\sqrt{2gh}-\frac{1}{2}g\)

Mà  \(s={{S}_{c}}\) nên ta có:

\(\sqrt{2gh}-0,5g=1,5g\Leftrightarrow \sqrt{2gh}=2g\Leftrightarrow h=2g=20m\)

Áp dụng công thức:

- Thời gian từ lúc rơi đến khi chạm đất: v = g.t

- Độ cao lúc thả vật:\(h = \frac{{g.{t^2}}}{2}\)

- Công thức độc lập với thời gian:

\(v_{^1}^2 - v_0^2 = 2g{h_1}\)

- Công thức vận tốc v = gt

Tóm tắt:

Tốc độc của vật khi chạm đất: \({{v}_{cd}}~=30m/s\)

Chọn gốc tọa độ tại vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống,  g = 10m/s ² .

Khi v = 20 (m/s) thì vật còn cách đất bao nhiêu và sau bao lâu thì vật rơi đến đất (kể từ khi tốc độ của vật là 20m/s).

Giải:

+ Thời gian từ lúc rơi đến khi chạm đất: \(v=g.t\Rightarrow t=3(s)\)

+ Độ cao lúc thả vật: \(h=\frac{g.{{t}^{2}}}{2}\Rightarrow h=45(m)\)

+ Khi tốc độ v ₁ = 20 m/s, ta có: \(v_{1}^{2}=2g{{h}_{1}}\Rightarrow {{h}_{1}}=20(m)\)

→ Vật cách mặt đất một đoạn: \(\Delta h=h-{{h}_{1}}=45-20=25(m)\)

+ Thời gian từ lúc thả đến khi vật đạt tốc độ là 20m/s là t ₁ :

\({{v}_{1}}=g.{{t}_{1}}\Rightarrow {{t}_{1}}=2(s)\Rightarrow {{t}_{2}}=t-{{t}_{1}}=1(s)\)

Phương trình chuyển động của vật có dạng tổng quát: \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a.{\left( {t - {t_0}} \right)^2}\)

Chọn gốc thời gian là lúc thả rơi vật. Gốc toạ độ ở mặt đất và chiều dương hướng xuống

Phương trình chuyển động của vật có dạng : \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a.{\left( {t - {t_0}} \right)^2}\)

Ta có: \(\left\{ \begin{array}{l}{y_0} = {y_M} =  - 50m\\{v_0} = 0\\{t_0} = 0\\a = g = 9,8m/{s^2}\end{array} \right. \Rightarrow y =  - 50 + \frac{1}{2}.10.{t^2} \Rightarrow y =  - 50 + 5{t^2}\,\,\left( m \right)\)

Phương trình chuyển động dạng tổng quát:  \(y = {y_0} + {v_0}\left( {t - {t_0}} \right) + \frac{1}{2}a{\left( {t - {t_0}} \right)^2}\)

Hai vật gặp nhau: y ₁ = y ₂

Chọn trục toạ độ thẳng đứng, gốc toạ độ tại đỉnh tháp, chiều dương hướng xuống.

Chọn gốc thời gian là lúc vật thứ nhất được thả rơi.

Phương trình chuyển động của vật (1): \({y_1} = {y_{01}} + {v_{01}}\left( {t - {t_{01}}} \right) + \frac{1}{2}{a_1}{\left( {t - {t_{01}}} \right)^2}\)

Có: \(\left\{ \begin{array}{l}{y_{01}} = 0\\{v_{01}} = 0\\{t_{01}} = 0\\{a_1} = g = 10m/{s^2}\end{array} \right. \Rightarrow {y_1} = 5{t^2}\,\,\,\left( m \right)\)

Phương trình chuyển động của vật (2): \({y_2} = {y_{02}} + {v_{02}}\left( {t - {t_{02}}} \right) + \frac{1}{2}{a_2}{\left( {t - {t_{02}}} \right)^2}\)

Có: \(\left\{ \begin{array}{l}{y_{02}} = 40m\\{v_{02}} = 0\\{t_{02}} = 2s\\{a_2} = g = 10m/{s^2}\end{array} \right. \Rightarrow {y_2} = 40 + 5{\left( {t - 2} \right)^2}\,\,\,\left( m \right)\)

Hai vật chạm nhau (gặp nhau): \({y_1} = {y_2} \Leftrightarrow 5{t^2} = 40 + 5{\left( {t - 2} \right)^2} \Rightarrow t = 3s\)

Sau 3s hai vật sẽ chạm nhau tính từ lúc vật thứ nhất được thả rơi

+ Sử dụng lí thuyết “Bài 4: Sự rơi tự do” – Trang 24 – SGK Vật Lí 10.

+ Thời gian vật rơi tự do: \(t = \sqrt {\dfrac{{2h}}{g}} \)

a) Các đặc điểm của sự rơi tự do:

+ Phương của chuyển động rơi tự do là phương thẳng đứng.

+ Chiều của chuyển động rơi tự do là chiều từ trên xuống dưới.

+ Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều

b) Thời gian giọt nước rơi tới mặt đất là:

\(t = \sqrt {\dfrac{{2h}}{g}}  = \sqrt {\dfrac{{2.45}}{{10}}}  = 3s\)

Vận dụng lí thuyết đã học

Số 1 chỉ bộ phận: máng đứng, có gắn dây dọi.

\(\begin{array}{l}g = \overline g  \pm \Delta g\\\delta g = \frac{{\Delta g}}{{\overline g }}.100\% \end{array}\)

\(\delta g = \frac{{\Delta g}}{{\overline g }}.100\%  = \frac{{0,002}}{{9,882}}.100\%  \approx 0,020\% \)

- Biểu thức tính tốc độ của vật trong rơi tự do: v = g.t

- Vận dụng lí thuyết tính sai số trong bài 3 sgk vật lí 10.

\(\overline v  = \overline g .t = 9,86.1,32 = 13,02(m/s)\)

Sai số:

\(\begin{array}{l}\overline {\Delta g}  = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3}}}{3} = \frac{{0,01 + 0,02 + 0}}{3} = 0,01(m/{s^2})\\\delta g = \frac{{\overline {\Delta g} }}{{\overline g }}.100\%  = \frac{{0,01}}{{9,86}}.100\%  = 0,1\% \\\delta t = \frac{{\overline {\Delta t} }}{t}.100\%  = \frac{{0,03}}{{1,32}}.100\%  = 2,3\% \\\delta v = \delta g + \delta t = 0,1\%  + 2,3\%  = 2,4\% \\\Delta v = \delta v.\overline v  = 2,4\% .13,02 = 0,31\\ \Rightarrow v = 13,02 \pm 0,31(m/s)\end{array}\)

Vận dụng lí thuyết trong sách giáo khoa

Các bước tiến hành thí nghiệm:

+ B1: Cắm nam châm điện vào ổ A và cổng quang điện vào ổ B ở mặt sai của đồng hồ đo thời gian hiện số

+ B2: Đặt MODE đồng hồ đo thời gian hiện số ở chế độ thích hợp

+ B3: Đặt trụ thép tại vị trí tiếp xúc với nam châm điện và bị giữ lại ở đó

+ B4: Nhấn nút RESET của đồng hồ MC964 để chuyển các số hiển thị về giá trị ban đầu 0.000

+ B5: Nhấn nút của hộp công tắc kép để ngắt điện vào nam châm điện: Trụ thép rơi xuống và chuyển động đi qua cổng quang điện.

+ B6: Ghi lại các giá rị thời gian hiển thị trên đồng hồ

+ B7: Dịch chuyển cổng quang điện ra xa dần nam châm điện, thực hiện lại các thao tác 3, 4, 5, 6 bốn lần nữa. Ghi lại các giá trị thời gian t tương ứng với quãng đường s.

=> Có 7 bước tiến hành thí nghiệm

Vận dụng kiến thức đã học

Cần đặt đồng hồ đo thời gian ở chế độ MODE A \( \leftrightarrow \) B để đo thời gian vật đi qua hai cổng quang điện.