Bài 1, 2, 3, 4 trang 104, 105 SGK Toán 4
Bài 1: Hãy nêu tên các cặp cạnh đối diện.
Bài 1
Hãy nêu tên các cặp cạnh đối diện trong: hình chữ nhật ABCD, hình bình hành EGHK, hình tứ giác MNPQ.
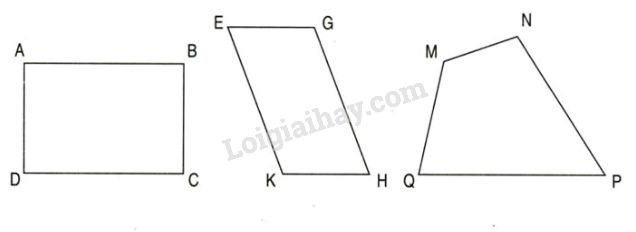
Phương pháp giải:
Quan sát kĩ các hình đã cho để tìm các cặp cạnh đối diện có trong mỗi hình vẽ đã cho.
Lời giải chi tiết:
Các cặp cạnh đối diện :
- Trong hình chữ nhật ABCD là : AB và CD, BC và AD.
- Trong hình bình hành EGHK là : EG và HK, GH và EK.
- Trong hình tứ giác MNPQ là : MN và PQ, NP và MQ.
Bài 2
Viết vào ô trống (theo mẫu)
|
Độ dài đáy |
7cm |
14dm |
23m |
|
Chiều cao |
16cm |
13dm |
16m |
|
Diện tích hình bình hành |
7 × 16 = 112 (cm 2 ) |
Phương pháp giải:
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
S = a × h
(S là diện tích, a là độ dài cạnh đáy, h là chiều cao hình bình hành).
Lời giải chi tiết:
|
Độ dài đáy |
7cm |
14dm |
23m |
|
Chiều cao |
16cm |
13dm |
16m |
|
Diện tích hình bình hành |
7 × 16 = 112 (cm 2 ) |
14 × 13 = 182 (dm 2 ) |
23 × 16 = 368 (m 2 ) |
Bài 3
Hình bình hành ABCD có độ dài cạnh AB là a, độ dài cạnh BC là b.

Công thức tính chu vi P của hình bình hành là:
P = (a + b) × 2 (a và b cùng một đơn vị đo)
Áp dụng công thức trên để tính chu vi hình bình hành, biết:
a) a = 8cm ; b = 3cm;
b) a = 10dm ; b = 5dm.
Phương pháp giải:
Thay chữ bằng số vào biểu thức P = (a + b) × 2 rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
a) Nếu a = 8cm ; b = 3cm thì chu vi hình bình hành là :
P = (8 + 3) × 2 = 22 (cm)
b) Nếu a = 10dm; b = 5dm thì chu vi của hình bình hành là :
P = (10 + 5) × 2 = 30 (dm)
Bài 4
Một mảnh đất trồng hoa hình bình hành có độ dài đáy là 40dm, chiều cao là 25dm. Tính diện tích của mảnh đất đó.
Phương pháp giải:
Áp dụng cách tính diện tích hình bình hành :
Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao (cùng một đơn vị đo).
Lời giải chi tiết:
Tóm tắt
Mảnh đất hình bình hành
Độ dài đáy: 40dm
Chiều cao: 25dm
Diện tích: ....?
Bài giải
Diện tích của mảnh đất đó là:
40 × 25 = 1000 (dm 2 )
Đáp số : 1000dm 2 .