Bài 1 trang 94 SGK Toán 11 tập 2 - Cánh diều — Không quảng cáo

Đề bài

$S.ABCD$ có $SA \bot \left( {ABCD} \right)$, đáy $ABCD$ là hình thoi cạnh $a$ và $AC = a$.

a) Tính số đo của góc nhị diện $\left[ {B,SA,C} \right]$.

b) Tính số đo của góc nhị diện $\left[ {B,SA,D} \right]$.

c) Biết $SA = a$, tính số đo của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$.

Lời giải chi tiết

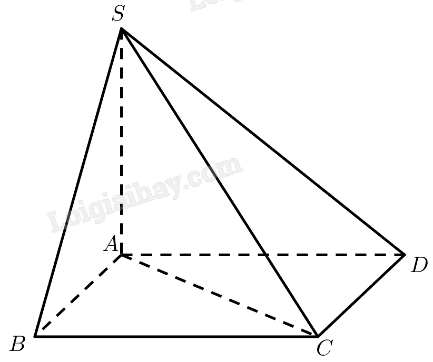
a) $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}$

Vậy $\widehat {BA{\rm{C}}}$ là góc phẳng nhị diện của góc nhị diện $\left[ {B,SA,C} \right]$

$AB = BC = AC = a \Rightarrow \Delta ABC$ đều $\Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }$

Vậy số đo của góc nhị diện $\left[ {B,SA,C} \right]$ bằng ${60^ \circ }$.

b) $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}$

Vậy $\widehat {BA{\rm{D}}}$ là góc phẳng nhị diện của góc nhị diện $\left[ {B,SA,D} \right]$

$ABCD$ là hình thoi $\Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }$

Vậy số đo của góc nhị diện $\left[ {B,SA,D} \right]$ bằng ${120^ \circ }$.

c) $SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}$

$\Delta SAC$ vuông tại $A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }$

Vậy $\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }$.