Bài 2 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho tứ diện đều (ABCD). Chứng minh rằng (AB bot CD).
Đề bài
Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\).
Phương pháp giải - Xem chi tiết
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
Lời giải chi tiết
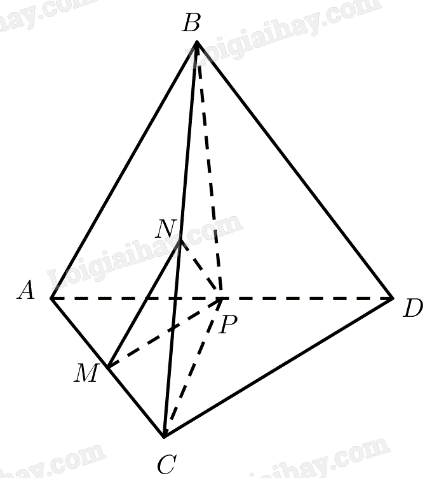
Giả sử tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AC,BC,A{\rm{D}}\).
\(M\) là trung điểm của \(AC\)
\(N\) là trung điểm của \(BC\)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel AB,MN = \frac{1}{2}AB = \frac{a}{2}\)
\(M\) là trung điểm của \(AC\)
\(P\) là trung điểm của \(AD\)
\( \Rightarrow MP\) là đường trung bình của tam giác \(AC{\rm{D}}\)
\( \Rightarrow MP\parallel C{\rm{D,MP}} = \frac{1}{2}C{\rm{D}} = \frac{a}{2}\)
Ta có: \(MN\parallel AB,MP\parallel C{\rm{D}} \Rightarrow \left( {AB,C{\rm{D}}} \right) = \left( {MN,MP} \right) = \widehat {NMP}\)
Ta có: \(BP\) là trung tuyến của tam giác \(ABD\)\( \Rightarrow BP = \frac{{\sqrt {2\left( {A{B^2} + B{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(CP\) là trung tuyến của tam giác \(ACD\)\( \Rightarrow CP = \frac{{\sqrt {2\left( {A{C^2} + C{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(NP\) là trung tuyến của tam giác \(BCP\)\( \Rightarrow NP = \frac{{\sqrt {2\left( {B{P^2} + C{{\rm{P}}^2}} \right) - B{C^2}} }}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác \(MNP\) có:
\(\cos \widehat {NMP} = \frac{{M{N^2} + M{P^2} - N{P^2}}}{{2.MN.MP}} = 0 \Rightarrow \widehat {NMP} = {90^ \circ }\)
Vậy \(\left( {AB,C{\rm{D}}} \right) = {90^ \circ }\).