Bài 3.6 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức
Điểm (0 - 9) (10 - 19) (20 - 29) (30 - 39) (40 - 49) Số thí sinh (1) (2) (4) (6) (15) Điểm (50 - 59) (60 - 69) (70 - 79) (80 - 89) (90 - 99) Số thí sinh (12) (10) (6) (3) (1)
Đề bài
Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:
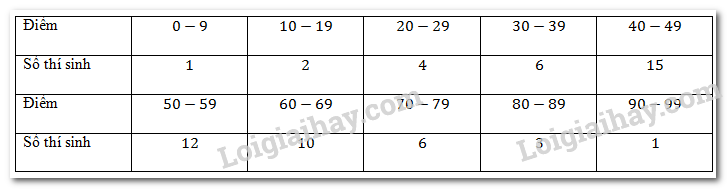
a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.
b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.
Phương pháp giải - Xem chi tiết
Để tính tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right).\;\)Khi đó,
\({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\) .
Trong đó, n là cỡ mẫu, \({m_p}\) là tần số nhóm p, với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Để tính tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\). Giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right)\). Khi đó,
\({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}}.\left( {{a_{p + 1}} - {a_p}} \right)\).
Trong đó, n là cỡ mẫu, \({m_p}\) là tần số nhóm p , với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Lời giải chi tiết
a)

b) Cỡ mẫu \(n = 60\)
Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{15}} + {x_{16}}}}{2}\). Do \({x_{15}},\;{x_{16}}\) đều thuộc nhóm \(\left[ {40;50} \right)\) nên nhóm náy chứa \({Q_1}\). Do đó,
\(p = 5;\;\;{a_5} = 40;\;\;{m_5} = 15;\;\;{m_1} + {m_2} + {m_3} + {m_4} = 1 + 2 + 4 + 6 = 13;\;{a_6} - {a_5} = 10\)
Ta có \({Q_1} = 40 + \frac{{\frac{{60}}{4} - 13}}{{15}} \times 10 = 41,33\)
Ý nghĩa: Có 25% số giá trị nhỏ hơn 41,33
Tứ phân vị thứ hai, \({M_e}\) là \(\frac{{{x_{30}} + {x_{31}}}}{2}\). Do \({x_{30}};\;{x_{31}}\) đều thuộc nhóm \(\left[ {50;60} \right)\) nên nhóm này chứa \({M_e}\). Do đó,
\(p = 6;\;\;{a_6} = 50;\;\;{m_6} = 12;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} = 1 + 2 + 4 + 6 + 15 = 13;\;{a_7} - {a_6} = 10\)
Ta có: \({Q_2} = 50 + \frac{{\frac{{60}}{2} - 28}}{{12}} \times 10 = 51,66\)
Ý nghĩa: Có 50% số giá trị nhỏ hơn 51,66
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{45}} + {x_{46}}}}{2}\). Do \({x_{45}},\;{x_{46}}\) đều thuộc nhóm \(\left[ {60;70} \right)\) nên nhóm náy chứa \({Q_3}\). Do đó,
\(p = 7;\;\;{a_7} = 60;\;\;{m_7} = 10;\;\;{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6} = 1 + 2 + 4 + 6 + 15 + 12 = 40; {a_8} - {a_7} = 10\).
Ta có: \({Q_3} = 60 + \frac{{\frac{{60 \times 3}}{4} - 40}}{{10}} \times 10 = 65\)
Ý nghĩa: Có 75% số giá trị nhỏ hơn 65.