Bài 3 trang 175 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Cho tam giác ABC nhọn. Về phía ngoài tam giác ABC vẽ tam giác BAD vuông cân tại A, tam giác CAE vuông cân tại A. Chung minh rằng :

a) DC = BE.

b) $DC \bot BE.$

c) $B{D^2} + C{E^2} = B{C^2} + D{E^2}.$

Lời giải chi tiết

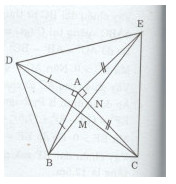
a)Ta có: $\eqalign{  & \widehat {BAE} = \widehat {CAE} + \widehat {BAC} = {90^0} + \widehat {BAC}  \cr  & \widehat {DAC} = \widehat {DAB} + \widehat {BAC} = {90^0} + \widehat {BAC} \cr}$

Nên $\widehat {BAE} = \widehat {DAC}$

Xét hai tam giác ADC và ABE có:

AD = AB (tam giác BAD vuông cân tại A)

$\widehat {DAC} = \widehat {BAE},AC = AE(\Delta CAE$  vuông cân tại A)

Do đó: $\Delta ADC = \Delta ABE(c.g.c) \Rightarrow CD = BE.$

b) Gọi M, N lần lượt là giao điểm của BE với CD, AC.

Ta có: $\widehat {ANE} + \widehat {AEN} = {90^0}(\Delta ANE$  vuông tại A).

Mà $\widehat {ANE} = \widehat {MNC}$   (đối đỉnh), $\widehat {AEN} = \widehat {MCN}(\Delta ADC = \Delta ABE)$

Suy ra $\widehat {MNC} + \widehat {MCN} = \widehat {ANE} + \widehat {AEN} = {90^0}.$

Tam giác CMN có: $\widehat {NMC} + \widehat {MNC} + \widehat {MCN} = {180^0}$

Do đó: $\widehat {NMC} = {180^0} - {90^0} = {90^0}.$   Vậy $CD \bot BE.$

Tam giác MBD vuông tại M $\Rightarrow B{D^2} = M{B^2} + M{D^2}$   (định lí Pythagore)

Tam giác MCE vuông tại M $\Rightarrow C{E^2} = M{C^2} + M{E^2}$   (định lí Pythagore)

Do đó: $B{D^2} + C{E^2} = M{B^2} + M{D^2} + M{C^2} + M{E^2}(1)$

Tam giác MBC vuông tại M $\Rightarrow B{C^2} = M{B^2} + M{C^2}$   (định lí Pythagore)

Tam giác MDE vuông tại M $\Rightarrow D{E^2} = M{D^2} + M{E^2}$   (định lí Pythagore)

Do đó: $B{C^2} + D{E^2} = M{B^2} + M{C^2} + M{D^2} + M{E^2}(2)$

Tà (1) và (2) ta có: $B{D^2} + C{E^2} = B{C^2} + D{E^2}$