Bài 37 trang 123 SGK Toán 9 tập 1
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC=BD.
Đề bài
Cho hai đường tròn đồng tâm \(O\). Dây \(AB\) của đường tròn lớn cắt đường tròn nhỏ ở \(C\) và \(D\). Chứng minh rằng \(AC=BD\).
Phương pháp giải - Xem chi tiết
+) Vẽ đường kính vuông góc với một dây.
+) Sử dụng tính chất: Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây ấy.
Lời giải chi tiết
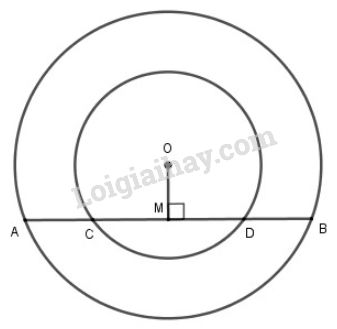
Vẽ \(OM\perp AB \Rightarrow OM \bot CD\).
Xét đường tròn \((O; OC)\) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và \(OM\perp CD\) nên M là trung điểm của CD hay \(MC=MD\) (định lý) (1)
Xét đường tròn \((O; OA)\) (đường tròn lớn) có OM là một phần đường kính, AB là dây và \(OM\perp AB\) nên M là trung điểm của AB hay \(MA=MB\) (định lý) (2)
Từ (1) và (2) \(\Rightarrow\) \(MA-MC=MB-MD\) \(\Rightarrow AC=BD.\)
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.