Bài tập 17 trang 129 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Hãy chứng minh rằng AB // CD trong mỗi hình dưới đây.

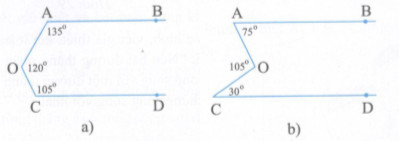
Lời giải chi tiết

a)

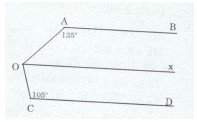
Kẻ đường thẳng Ox // CD qua O

Ta có: Ox // CD (cách vẽ)

$\Rightarrow \widehat {xOC} + \widehat {OCD} = {180^0}$  (hai góc trong cùng phía)

$\eqalign{  &  \Rightarrow \widehat {xOC} = {180^0} - {105^0} = {75^0}  \cr  & \widehat {A0x} + \widehat {xOC} = {120^0}(vi\widehat {AOC} = {120^0})  \cr  &  \Rightarrow \widehat {A0x} = {120^0} - {75^0} = {45^0}  \cr  & \widehat {BAO} + \widehat {A0x} = {135^0} + {45^0} = {180^0} \cr}$

Mà hai góc BAO và Aox nằm ở vị trí trong cùng phía và bù nhau => AB // Ox

Mặt khác: Ox // CD (cách vẽ) nên ta có: AB // CD.

b)

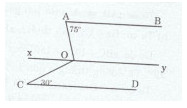
Kẻ đường thẳng xy qua điểm O và song song với CD

Ta có: $\widehat {xOC} = \widehat {OCD} = {30^0}(\widehat {xOc}va\widehat {OCD}$  là hai góc so le trong và xy // CD)

$\eqalign{  & \widehat {A0x} + \widehat {xOC} = \widehat {AOC} = {105^0}  \cr  &  \Rightarrow \widehat {A0x} = {105^0} - {30^0} = {75^0} \cr}$

Mà $\widehat {BAO} = {75^0}.$  Nên $\widehat {A0x} = \widehat {BAO}$

Do hai góc ở vị trí so le trong nên AB // xy

Mặt khác: xy // CD (cách vẽ) nên ta có: AB // CD.