Bài tập 17 trang 116 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Cho góc tù xOy. Trong góc xOy vẽ tia Om vuông góc với Ox và tia On vuông góc với tia Oy.

a) Chứng tỏ rằng $\widehat {xOn} = \widehat {mOy}$

b) Tính số đo góc $\widehat {xOy} + \widehat {mOn}$

c) Gọi Ot là tia phân giác của góc xOy. Chứng minh rằng Ot là tia phân giác của góc mOn.

Lời giải chi tiết

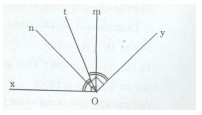
a)Ta có: $Om \bot 0x \Rightarrow \widehat {m0x} = {90^0}$  và $On \bot Oy \Rightarrow \widehat {nOy} = {90^0}$

Do đó: $\widehat {m0x} = \widehat {nOy}({90^0})(1)$

Tia On nằm trong $\widehat {xOy} \Rightarrow \widehat {xOn} + \widehat {nOy} = \widehat {xOy}$

Và tia Om nằm trong $\widehat {xOy} \Rightarrow \widehat {mOy} + \widehat {m0x} = \widehat {xOy}$

Nên $\widehat {xOn} + \widehat {nOy} = \widehat {mOy} + \widehat {m0x}(2)$

Từ (1) và (2) ta có: $\widehat {xOn} = \widehat {mOy}$

b) Ta có: $\eqalign{  & \widehat {xOy} + \widehat {mOn} = \widehat {nOy} + \widehat {xOn} + \widehat {mOn}  \cr  &  = {90^0} + \widehat {mOy} + \widehat {mOn} = {90^0} + \widehat {nOy} = {90^0} + {90^0} = {180^0} \cr}$

c) Ta có: Ot là tia phân giác góc $\widehat {xOy} \Rightarrow \widehat {xOt} = \widehat {yOt} \Rightarrow \widehat {xOn} + \widehat {nOt} = \widehat {yOm} + \widehat {mOt}$

Mà $\widehat {xOn} = \widehat {mOy}$  (câu a) $\Rightarrow \widehat {nOt} = \widehat {mOt}$

Mà tia Ot nằm giữa hai tia Om và On => Ot là tia phân giác góc mOn.