Bài tập 2 trang 118 Tài liệu dạy – học Toán 7 tập 1 — Không quảng cáo

Đề bài

Vẽ trên cùng một hình:

a) Góc xOy có số đo bằng 60 ^o

b) Góc x’Oy’ đối đỉnh với góc xOy.

c) Tia phân giác Ot của góc xOy.

d) Tia Ot’ là tia đối của tia Ot.

- Tia Ot’ có là tia phân giác của góc x’Oy’ không ?

- Viết tên 6 cặp góc đối đỉnh và tính số đo của mỗi góc đó.

Lời giải chi tiết

a)b)c)

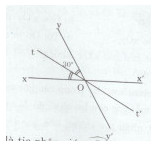
d) Ta có: $\widehat {xOt} = \widehat {yOt}$  (Ot là tia phân giác góc xOy)

$\widehat {xOt} = \widehat {x'Ot'}$  (đối đỉnh) và $\widehat {yOt} = \widehat {y'Ot'}$  (đối đỉnh) $\Rightarrow \widehat {x'Ot'} = \widehat {y'Ot'}$

Mà tia Ot’ nằm giữa hai tia Ox’, Oy’. Vậy Ot’ là tia phân giác của góc xOy

Có 6 cặp góc đối đỉnh là:

xOt và x’Ot’; yOt và y’Ot’; x’Oy và xOy’

xOy và x’Oy’; x’Ot và xOt’; y’Ot và yOt’.

Ta có: $\widehat {xOt} = \widehat {yOt} = {1 \over 2}\widehat {xOy} = {30^0}$  (Ot là tia phân giác góc xOy)

$\widehat {xOy} + \widehat {x'Oy} = {180^0}$  (kề bù)

Do đó: $\widehat {x'Oy} = {180^0} - \widehat {xOy} = {180^0} - {60^0} = {120^0}$

$\widehat {yOt'} + \widehat {yOt} = {180^0}$  (kề bù) $\Rightarrow \widehat {yOt'} = {180^0} - \widehat {yOt} = {180^0} - {30^0} = {150^0}$

Và $\widehat {x'Ot} + \widehat {xOt} = {180^0}$  (kề bù) $\Rightarrow \widehat {x'Ot} = {180^0} - \widehat {xOt} = {180^0} - {30^0} = {150^0}$

$\widehat {x'Ot'} = \widehat {xOt} = {30^0}$  (hai góc đối đỉnh)

$\widehat {y'Ot'} = \widehat {yOt} = {30^0}$

$\widehat {xOy'} = \widehat {x'Oy} = {120^0}$  (hai góc đối đỉnh)

$\widehat {x'Oy'} = \widehat {xOy} = {60^0}$  (hai góc đối đỉnh)

$\widehat {y'Ot} = \widehat {yOt'} = {150^0}$  (hai góc đối đỉnh)

$\widehat {xOt'} = \widehat {x'Ot} = {150^0}$  (hai góc đối đỉnh)