Bài tập 21 trang 154 Tài liệu dạy – học Toán 7 tập 1
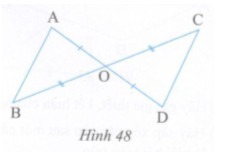
Giải bài tập Ở hình 48 cho biết OA = OD, OB = OC. Chứng minh rằng AB = CD và AB // DC.
Đề bài
Ở hình 48 cho biết OA = OD, OB = OC. Chứng minh rằng AB = CD và AB // DC.
Lời giải chi tiết
Xét tam giác AOB và DOC có:
OA = OD (gt)
OB = OC (gt)
\(\widehat {AOB} = \widehat {DOC}\) (hai góc đối đỉnh)
Do đó: \(\Delta AOB = \Delta DOC(c.g.c) \Rightarrow AB = CD,\widehat {OAB} = \widehat {ODC}\)
Ta có: \(\widehat {OAB} = \widehat {ODC}.\)
Mà \(\widehat {OAB}\) và \(\widehat {ODC}\) ở vị trí so le trong
\(\Rightarrow AB // CD\).
Cùng chủ đề:
Bài tập 21 trang 154 Tài liệu dạy – học Toán 7 tập 1