Bài tập 29 trang 98 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Tam giác ABC cân tại A, trên cạnh BC lấy các điểm D, E sao cho BD = DE = EC. Chứng minh rằng trong ba góc BAD, DAE, EAC thì góc DAE là góc lớn nhất.
Đề bài
Tam giác ABC cân tại A, trên cạnh BC lấy các điểm D, E sao cho BD = DE = EC. Chứng minh rằng trong ba góc BAD, DAE, EAC thì góc DAE là góc lớn nhất.
Lời giải chi tiết
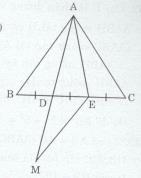
Xét ∆ABD và ∆ACE có: AB = AC (∆ABC cân tại A)
\(\widehat {ABD} = \widehat {ACE}\) (∆ABC cân tại A)
BD = EC (gt)
Do đó ∆ABD = ∆ACE (c.g.c) \( \Rightarrow \widehat {BAD} = \widehat {EAC}\)
Ta có \(\widehat {AEB} > \widehat C(\widehat {AEB}\) là góc ngoài của tam giác ACD)
\(\widehat C = \widehat B\) (∆ABC cân tại A)
Nên \(\widehat {AEB} > \widehat B\)
∆ABE có \(\widehat {AEB} > \widehat B\) => AB > AE
Trên tia đối của tia DA lấy điểm M sao cho DM = DA
Xét ∆DME và ∆DAB có DM = DA, \(\widehat {MDE} = \widehat {ADB}\) (đối đỉnh), DE = BD (gt)
Do đó ∆DME = ∆DAB (c.g.c) \( \Rightarrow ME = AB,\widehat {DME} = \widehat {BAD}\)
Ta có ME > AE. ∆AEM có ME > AE \( \Rightarrow \widehat {DAE} > \widehat {DME}\)
Nên \(\widehat {DAE} > \widehat {BAD} = \widehat {EAC}.\)
Vậy trong ba góc BAD, DAE, EAC thì góc DAE lớn nhất.