Bài tập 4 trang 127 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A
Đề bài
Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^o}} \right)\). Hai đường cao BE, CF cắt nhau tại H.
a) Chứng minh rằng \(\Delta BEC = \Delta CFB\)
b) Chứng minh rằng \(\Delta AHF = \Delta AHE\)
c) Gọi I là trung điểm của BC. Chứng minh rằng A, H, I thẳng hàng.
Lời giải chi tiết
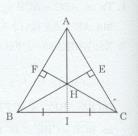
a) Xét ∆BEC (\(\widehat E = 90^\circ\)) và ∆CFB (\(\widehat F = 90^\circ\)) ta có:
BC (cạnh chung) và \(\widehat {BCE} = \widehat {CBF}\) (∆ABC cân tại A).
Do đó: ∆BEC = ∆CFB (cạnh huyền – góc nhọn).
b) Ta có: AB = AC (∆ABC cân tại A).
BF = CE (∆CBF = ∆BEC).
=> AB – BF = AC – CE => AF = AE.
Xét ∆AHF (\(\widehat F = 90^\circ\)) và ∆AHE (\(\widehat E = 90^\circ\)) ta có:
AH (cạnh chung) và AF = AE.
Do đó: ∆AHF = ∆AHE (cạnh huyền – cạnh góc vuông).
c) ∆ABC có hai đường cao BE và CF cắt nhau tại H (gt)
=> H là trực tâm của ∆ABC => AH là đường cao của ∆ABC
Mà ∆ABC cân tại A. Nên AH cũng là đường trung tuyến của ∆ABC
Lại có I là trung điểm của BC (gt). Nên A, H, I thẳng hàng.