Bài tập 4 trang 130 Tài liệu dạy – học Toán 7 tập 2 - Hình học
Giải bài tập Tam giác ABC vuông tại A (AB < AC)
Đề bài
Tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ \(BE \bot AN\,\,\left( {E \in AN} \right)\)
a) Chứng minh BE là tia phân giác của góc ABN.
b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh NK // CA.
c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh tam giác GBC cân.
Lời giải chi tiết
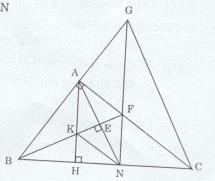
a) BA = BN => ∆ABN cân tại B.
Mà BE là đường cao của ∆ABN (vì \(BE \bot AN\) tại E)
Nên BE cũng là đường phân giác của ∆ABN
Vậy BE là tia phân giác của \(\widehat {ABN}.\)
b) ∆ABN có hai đường cao BE và AH cắt nhau tại K (gt).
=> K là trực tâm của ∆ABN
=> NK là đường cao của ∆ABN
\( \Rightarrow NK \bot AB\)
Mà \(CA \bot AB\) (∆ABC vuông tại A)
Nên NK // CA.
c) Ta có: \(\widehat {NFC} = \widehat {FNK}\) (hai góc so le trong và NK // AC)
\(\widehat {NFC} = \widehat {AFG}\) (đối đỉnh)
\( \Rightarrow \widehat {FNK} = \widehat {AFG}\)
Mà \(\widehat {FNK}\) và \(\widehat {AFG}\) ở vị trí đồng vị. Nên AH // GN
Lại có \(AH \bot BC\) (AH là đường cao của ∆ABC) \( \Rightarrow GN \bot BC.\)
Xét ∆ABC và ∆GNB ta có \(\widehat {BAC} = \widehat {BNG}( = 90^\circ )\)
AB = BN (gt)
\(\widehat {ABC}\) chung
Do đó: ∆ABC = ∆NBG (g.c.g) => BC = BG
Vậy ∆BGC cân tại B.